TitelScheitelpunktform
Autoranonym
veröffentlicht28.10.2025
FachMathematik
KompetenzbereichFunktionen
NiveaustufeR (Regelstandard)
Phase9
MaterialformInputmaterial

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

In diesem Kapitel des Lernpfads wirst du Experte für die Scheitelpunktform quadratischer Funktionen. Du kannst

selbstständig mithilfe der vorliegenden Applets reale Flugkurven, Gebäude oder Phänomene aus der Natur modellieren,
in einem Zuordnungsquiz selbst überprüfen, ob du alles verstanden hast, und
abschließend in Partnerarbeit Flugkurven in verschiedenen Sportarten untersuchen.

Schau dir das GeoGebra Applet an und wiederhole noch einmal die Auswirkungen aller 3 Parameter auf den Graphen der Funktion:

Bearbeite anschließend folgendes Applet:

Als Beispiel ist der Funktionsterm

y = 0, 5 (x + 1)^{2} - 2

einer quadratischen Funktion in Scheitelpunktform gegeben. Skizziere den zugehörigen Graphen in das Koordinatensystem.

Hinweis

Denke noch mal daran, was die Parameter a,d und e einzeln für eine Auswirkung auf die Lage des Graphen einer Funktion haben. Notiere deine Überlegungen. Kombiniert ergeben sie die Lage des Graphen der Funktion in Scheitelpunktform.

Lösung:

Der Parameter $a = 0, 5$ ist größer als Null aber kleiner als Eins, weshalb die Parabel nach oben geöffnet und gestaucht ist.

Da im Funktionsterm $(x + 1)^{2}$ steht, ist der Parameter d=−1 negativ. Die Parabel ist also um eine Einheit in negative x-Richtung verschoben ist.

Der Parameter $e = - 2$ ist negativ, weshalb die Parabel um zwei Einheiten in positive y-Richtung verschoben ist.

Merke

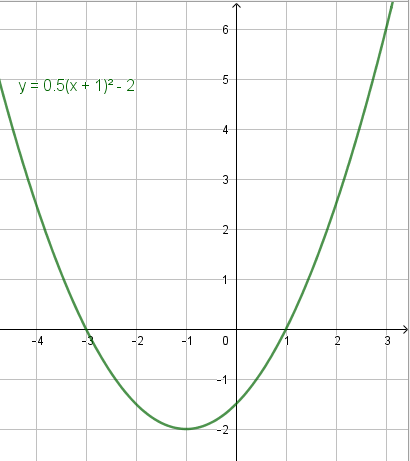
Terme quadratischer Funktionen können in der Form $y = a (x - d)^{2} + e$ angegeben werden (wobei a ≠ 0). Diese Darstellungsform nennt man Scheitelpunktform, da sich direkt aus dem Term der Scheitelpunkt ablesen lässt. Er hat die Koordinaten $S (d / e)$ .

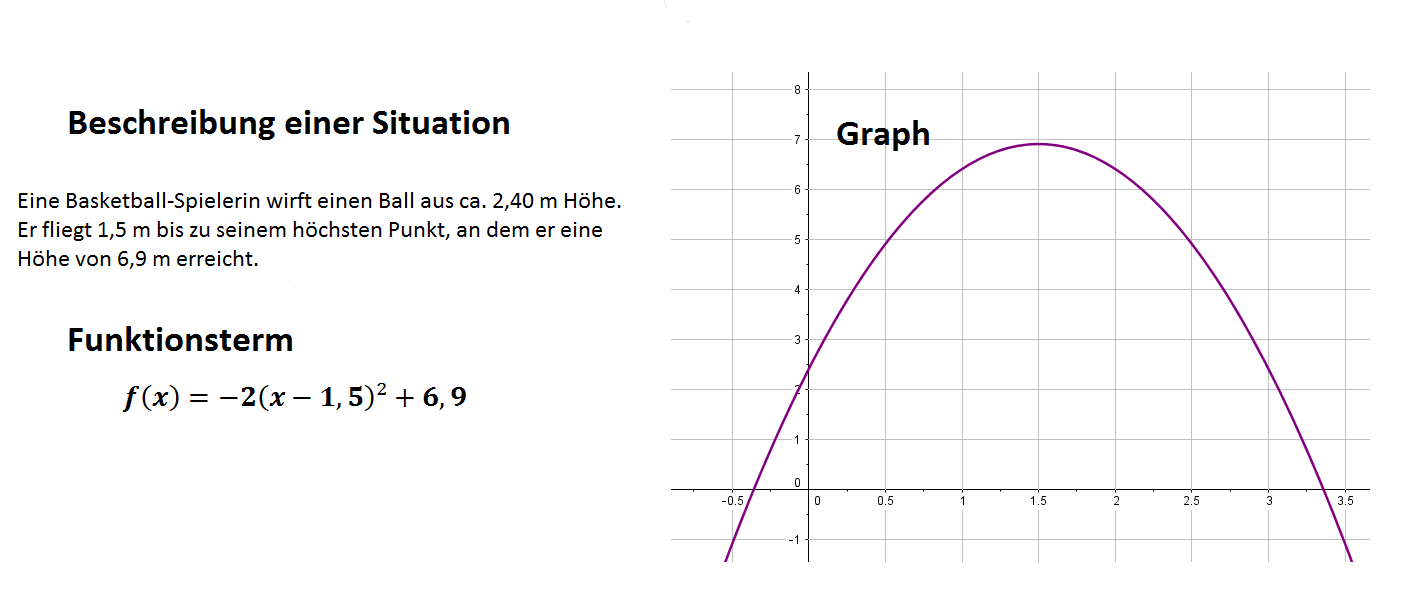
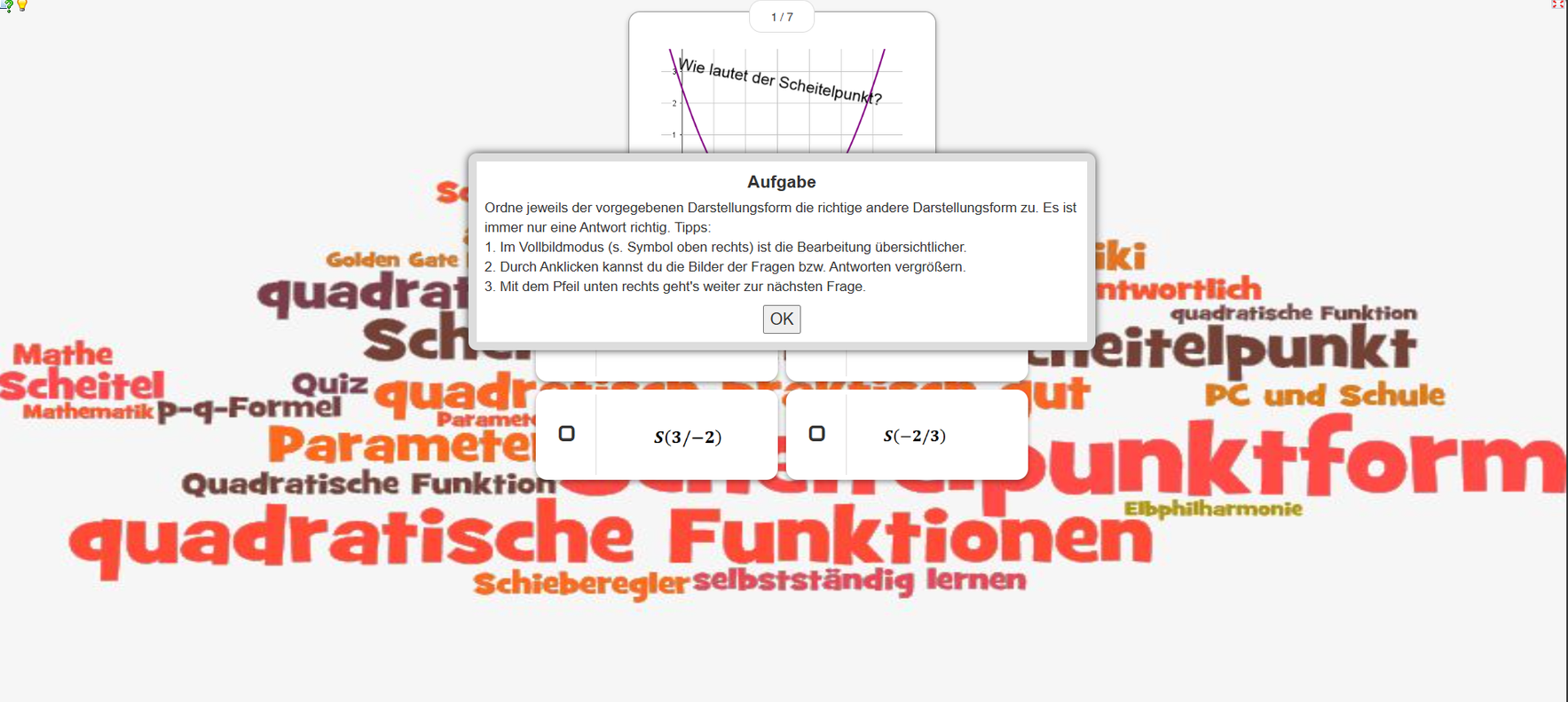
Das folgende Quiz beschäftigt sich mit dem Wechsel zwischen verschiedenen Darstellungsarten (Funktionsterm, Graph und Situationen) quadratischer Funktionen. Hier ist für die drei Darstellungsarten zum Thema Basketball ein Beispiel dargestellt:

Bearbeite das folgende Quiz:

https://learningapps.org/watch?v=pozha6j7n16