Einführung

Für welchen Spieler soll sie sich entscheiden?
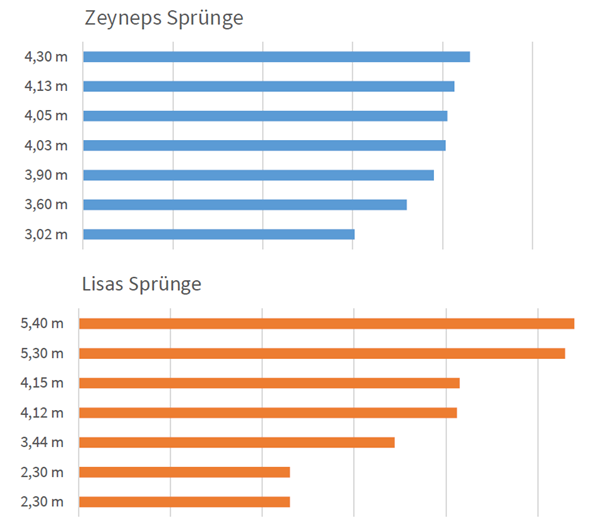
Ihre Trainerin Paula Müller hat die Leistungen in Diagrammen dargestellt. Wer von beiden zeigt die bessere Leistung?
- Finde verschiedene Argumente für die jeweiligen Springerinnen
- Für welche Weitspringerin würdest du dich entscheiden?
https://editor.mnweg.org/entdecken/dokument/varianz-und-standardabweichung
https://editor.mnweg.org/entdecken/dokument/varianz-und-standardabweichung
Varianz und Standardabweichung
Zwei Oberstufenschüler Max und Moritz aus Geithain vergleichen ihre Stundenpläne. Beide habe 34 Wochenstunden. Diese sind jedoch sehr unterschiedlich verteilt (Angaben in Stunden).
Wochentag
Mo
Di
Mi
Do
Fr
Max
4
6
4
10
10
Moritz
6
10
8
4
6
Wenn du nun bewerten solltest, welcher Stundenplan der besser ist, dann fiele dir die Entscheidung vermutlich leicht.
Möchte man das mit Hilfe unserer Lageparameter arithmetische Mittel, Median, Minimum und Maximum nachweisen, so stellt man fest, dass alle Parameter gleich sind:
Lageparameter
Max
Moritz
Arithmetisches
Mittel xˉ
6,8
6,8
Median
6
6
Minimum xmin
4
4
Maximum xmax
10
10
Spannweite w
6
6
Wir brauchen also noch einen weiteren Steuungsparameter: Die Standardabweichung s. Um diese jedoch zu definieren, hat man einen Zwischenwert bei der Berechnung eingeführt: Die Varianz s2. Sie ist der mittlere quadratische Abstand vom arithmetischen Mittel. Das klingt kompliziert, ist es aber nicht.
Wir nehmen die Differenz der einzelnen Messwerte vom arithmetischen Mittel xˉ = 6,8 für den Stundenplan von Max. Also ergibt sich:
4 - 6,8 = -2,8
6 - 6,8 = -0,8
4 - 6,8 = -2,8
10 - 6,8 = 3,2
10 - 6,8 = 3,2
Nun hat man sowohl positive als auch negative Werte. Um dies zu vermeiden, hielt man es für sinnvoller, anstatt Betragsstriche zu setzen, die Werte zu quadrieren. Anschließend summiert man die Werte auf und dividiert durch n (Anzahl der Werte), um den Mittelwert zu bilden.
Varianz(s2)=5(−2,8)2+(−0,8)2+(−2,8)2+3,22+3,22=7,4
https://editor.mnweg.org/entdecken/dokument/varianz-und-standardabweichung
Um nun die Quadration rückgängig zu manchen, zieht man die Wurzel und erhält die Standardabweichung s.
Standardabweichungs=s2=7,4=2,7
Die errechnete Standardabweichung bedeutet, dass die Werte von Max im Mittel um 2,7 vom arithmetischen Mittel (Durchschnitt) abweichen.
Für eine Stichprobe mit Umfang n und arithmetischem Mittel xˉ gilt für die Varianz:
s2=n(x1−xˉ)+(x2−xˉ)+...+(xn−xˉ)2
Die Standardabweichung ist s=s2
Berechnen wir nun die Varianz und Standardabweichung für den Stundenplan von Moritz:
s2=5(6−6,8)2+(10−6,8)2+(4−6,8)2+(6−6,8)2=3,9
s=3,9=2,0
Wir sehen also, dass die Standardabweichung bei Moritz (s = 2,0) kleiner ist als die bei Max (s = 2,7), so dass man daraus schließen kann, dass Moritz Stundenzahl weniger vom Mittelwert abweicht als die von Max.
1. Durchschnitte der Spieler einzeln berechnen
2. Jeweils die Abweichung vom Mittelwert nehmen und quadrieren (Klammern nicht vergessen!
3. Für die Standardabweichung noch die Wurzel ziehen
https://editor.mnweg.org/entdecken/dokument/varianz-und-standardabweichung


