In diesem Kapitel kannst du herausfinden, wie du quadratische Funktionen in Scheitelpunktform in quadratische Funktionen in Allgemeine Form umwandeln kannst.
Wiederholung: Binomische Formeln
Die 1. binomische Formel ist:
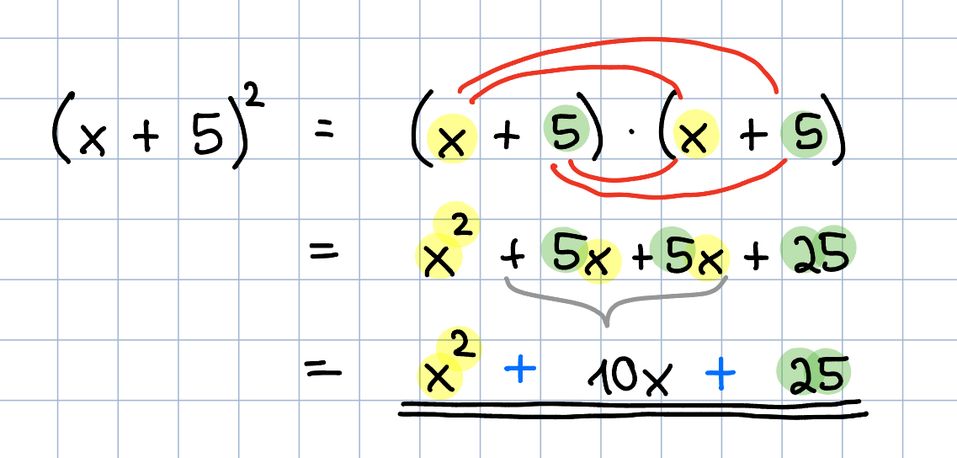
Die 2. binomische Formel ist:
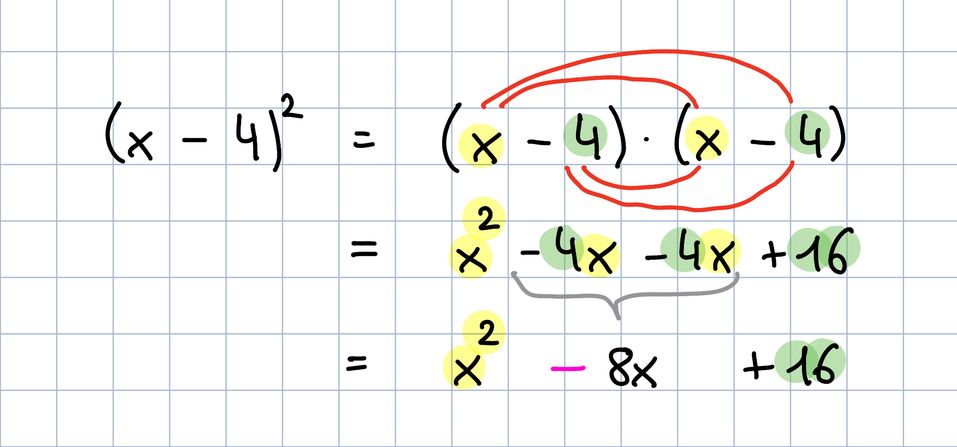
Die 3. binomische Formel ist:
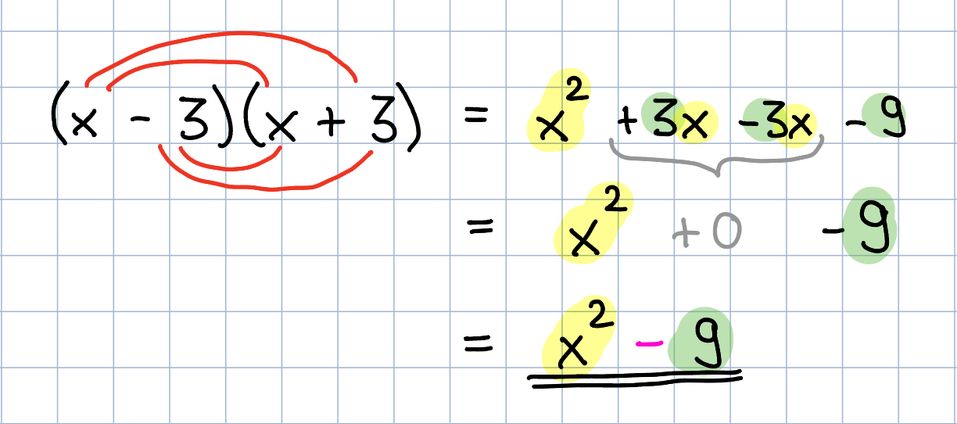
https://editor.mnweg.org/entdecken/dokument/von-der-scheitelpunkt-zur-normalform
Mithilfe der binomischen Formeln lassen sich Funktionen der Form f(x)=a(x−d)2 in die Allgemeine Form f(x)=ax2+bx+c umwandeln:
Beispiel 1: f(x)=(x−2)2=x2−4x+4
Beispiel 2: f(x)=(x−1)2=x2−2x+1
Beispiel 3: f(x)=2(x+1)2+1
Schritt
Anleitung
Funktionsterm
1
Klammer auflösen mithilfe einer binomischen Formel
f(x)=2(x2+2x+1)+1
2
Klammer ausmultiplizieren
f(x)=(2x2+4x+2)+1
3
Zusammenfassen
f(x)=2x2+4x+3
Erklärvideo
Falls dir die Umformung von der Scheitelpunkt- auf die Allgemeine Form schwer fiel, kannst du dir hier ein Video dazu anschauen und es dann noch einmal probieren. Denke daran dir Kopfhörer anzuziehen, sofern du nicht alleine in einem Raum bist.
Quadratische Funktionen können auf verschiedene Weisen in Termen dargestellt werden. Die beiden Formen, die du bisher kennengelernt hast, heißen
Scheitelpunktform und
Allgemeine Form.
Eine Parabel kann immer in beiden Darstellungsformen beschrieben werden.
Durch Ausmultiplikation des Terms einer quadratischen Funktion in Scheitelpunktform erhält man den zugehörigen Term in Allgemeiner Form.
https://editor.mnweg.org/entdecken/dokument/von-der-scheitelpunkt-zur-normalform


