TitelWurzeln
Autoranonym
veröffentlicht13.07.2025
FachMathematik
KompetenzbereichZahlen
NiveaustufeM (Mindeststandard)
Phase9
MaterialformInformation

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Wurzeln

Bisher haben wir uns immer allgemein mit Wurzeln beschäftigt, z.B.:

$16 = 4$ oder $36 = 6$ oder $144 = 12$

Hierbei handelt es sich eigentlich um Beispiele für Quadratwurzeln. Warum? Weil wir die Zahl gesucht haben, die mit sich selbst multipliziert (= quadriert) die Zahl unter der Wurzel ergibt. Hier also:

$16 = 4$ , denn $4 \cdot 4 = 4^{2} = 16$

$36 = 6$ , denn $6 \cdot 6 = 6^{2} = 36$

$144 = 12$ , denn $12 \cdot 12 = 1 2^{2} = 144$

Man schreibt deshalb auch $216$ , $236$ oder $2144$ .

Was ist aber das Ergebnis von $38$ ? Denke kurz drüber nach. Das Ergebnis steht auf der nächsten Seite.

Die Antwort ist: 2, also:

$38 = 2$ , denn $2 \cdot 2 \cdot 2 = 2^{3} = 8$

Beim Rechnen mit Wurzeln sind folgende Begriffe wichtig:

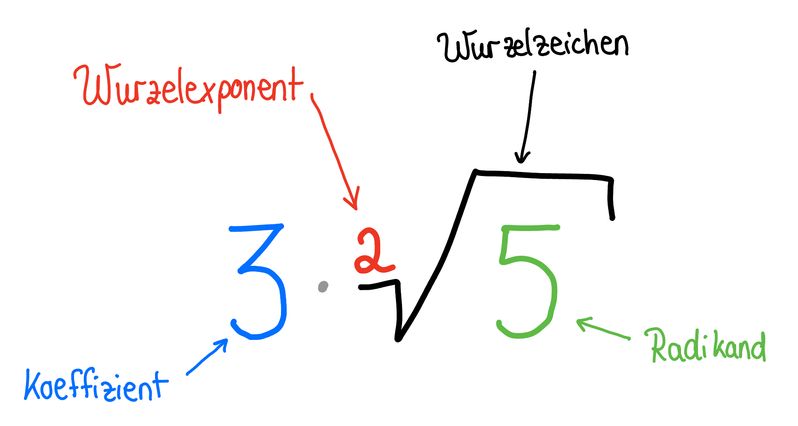
Wenn kein Wurzelexponent angegeben ist,

hat die Wurzel den Wurzelexponenten 2.

Merke

$25 = 225 = 5$ , denn $5 \cdot 5 = 5^{2} = 25$

$416 = 2$ , denn $2^{4} = 16$

$327 = 3$ , denn $3 \cdot 3 \cdot 3 = 3^{3} = 27$

$\frac{4}{9} = \frac{2}{3}$ , denn $\frac{2}{3} \cdot \frac{2}{3} = (\frac{2}{3})^{2} = \frac{4}{9}$

$3 - 8 = ⊘$ , denn aus negativen Zahlen können keine Wurzeln gezogen werden

n-te Wurzel ziehen OHNE Taschenrechner – 3. Wurzel im Kopf rechnen

YouTube-Video

Wur­zeln

Wurzeln