Willkommen im Baustein Zuordnungen im Alltag
Nach diesem Baustein...
... kannst du Daten sammeln und auf verschiedene Arten darstellen.
... weißt du, was Zuordnungen sind und wie sie dargestellt werden können.
... weißt du, was ein Graph ist und wie du ihn interpretieren kannst.
Aufbau des Bausteins:
benötigtes Material:
(hier brauchst du eine:n Arbeitspartner:in) (90min)
Buntstifte
Stoppuhr
Schere
Klebestift
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
Teste dein Wissen!
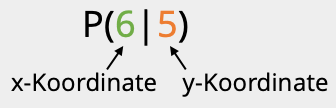
... wie ein Punkt notiert wird?
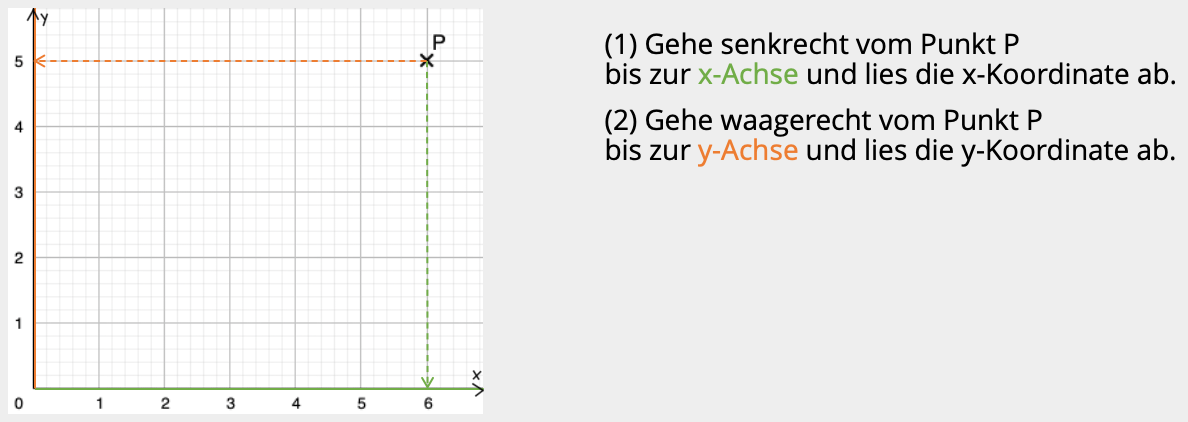
... wie du einen Punkt im Koordinatensystem ablesen kannst?
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
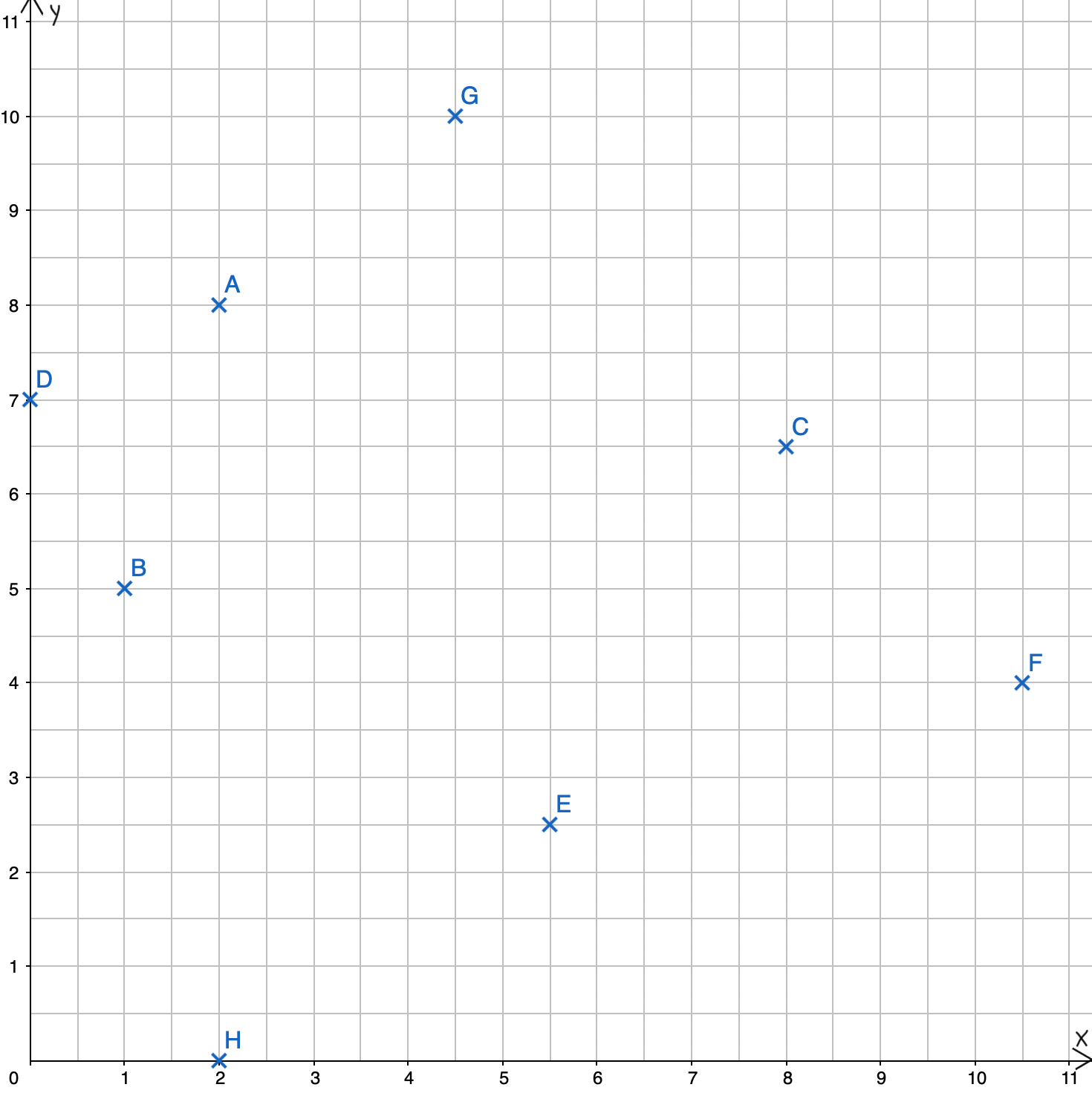
... wie du Punkte in einem Koordinatensystem einträgst?

hat ihr deswegen eine Anleitung geschrieben,
wie sie einen Fisch am besten zeichnen kann.
Hilf Maja die Zeichnung zu vervollständigen.
- Trage die folgenden Punkte nacheinander in das Koordinatensystem ein und verbinde sie in der angegebenen Reihenfolge.
a. A(7|11), B(5|13), C(3|11), D(2|9), E(2|7), F(4|7), G(5|9), A(7|11).
b. H(3|5), I(0|6), J(0|1), K(3|3), H(3|5)
c. K(3|3), L(2|1), ;M(4|0), N(6|2), O(6|3), P(4|4), K(3|3)
d. Q(6|0),R(8|0),S(10|1),T(11|3),U(9|2),N(6|2),Q(6|0) - Trage den Punkt M₁ (9|9) ein und zeichne um diesen Punkt freihändig einen kleinen Kreis, der etwa so groß ist wie der Halbkreis daneben. Male um den Mittelpunkt M₁ dieses Kreises einen stecknadelkopfgroßen schwarzen Punkt.
- Verbinde den Punkt F(4|7) mit dem Punkt H(3|5).
- Verbinde den Punkt T(11|3) mit dem Punkt V(12|4) und dem Punkt W(12|5).
- Trage die Punkte X(12|6), Y(11|5), Z(10|5) und A₁(8|7) in das Koordinatensystem ein. Versuche, die Punkte nicht gerade, sondern bogenförmig zu verbinden.
- Trage die Punkte B₁(12|8) und C₁(9|11) ein und verbinde B₁, C₁ und A(7|11).
- Male den Fisch nun mit deinen Lieblingsfarben aus.
Kopiervorlage 1
Buntstifte

https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
Versenke die Schiffe deines Partners.
- Anleitung:
In das linke Koordinatensystem zeichnet sich jeder seine Schiffsflotte ein. Sie besteht aus einem 5er, einem 4er, zwei 3er und zwei 2er Schiffen. Die Schiffe dürfen sich nicht berühren.
Das rechte Koordinatensystem ist das Kontrollsystem für schon abgeschossene Koordinaten des gegnerischen Kapitäns.
Nachdem jeder Kapitän seine Schiffe gesetzt hat, fängt der größere Kapitän an, die Schiffe seines „Gegners“ ins Visier zu nehmen. Dafür nennt er einen Koordinatenpunkt. Der Gegenspieler überprüft nun seine Schiffe und teilt mit, ob er getroffen wurde oder ob der Schuss ins Wasser ging.
Dieser Punkt wird rot (bei einem Treffer) oder blau (bei einem Schuss ins Wasser) im rechten Koordinatensystem eingetragen, um im weiteren Spielverlauf einen Überblick zu haben, welche Punkte schon abgeschossen wurden.
Ging der Schuss daneben, ist der andere Kapitän an der Reihe. Wurde hingegen ein Teil des Schiffes getroffen, darf weiter geschossen werden.
Kopiervorlage 2 (jeder Spieler bekommt eine Hälfte des Blattes)
blaue und rote Stifte
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
Einführung Zuordnungen im Alltag
Die Klasse 6b der Sportschule plant ihre Klassenfahrt. Die Schüler und Schülerinnen wollen mit dem Fahrrad zum Schullandheim fahren. Es fahren drei Lehrkräfte mit, die jeweils eine Gruppe begleiten, damit nicht zu viel Chaos entsteht.
Der Klassenleiter Herr Friedrich teilt die Gruppen wie folgt ein:
Name
Gruppe
Name
Gruppe
Name
Gruppe
Name
Gruppe
Anna
2
Sophie
2
Hans
2
Paul
1
Jonas
3
Sina
1
Lara
1
Chris
1
Emilie
3
Greta
1
Karl
3
Julia
3
Peter
2
Sarah
3
Klara
2
Um den Überblick zu behalten, notiert Herr Friedrich die Gruppenzugehörigkeit als Zuordnung (Name → Gruppe) wie folgt:
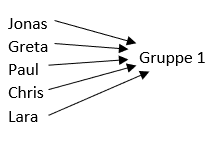
Bei einer Zuordnung wird einem Ausgangswert ein oder mehrere Zielwerte zugeordnet.
Jedem x-Wert wird beispielsweise ein y-Wert zugeordnet. Dieses Paar heißt auch Wertepaar.
Zum Beispiel wird Jonas der Gruppe 1 zugeordnet (Jonas → Gruppe 1)
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
Klara und Peter unterhalten sich über den Tagesplan.
Klara schlägt vor:
„Wie wäre es, wenn wir um 9:00 Uhr auf dem Schulhof starten und nach 1 Stunde am See frühstücken? Zum See sind es 15 km. Nach einer halben Stunde könnten wir dann weiter in Richtung des 25 km entfernten Ortes fahren. Dort arbeitet meine Mutter in einem Restaurant, wo wir direkt Mittagsessen können. Den Tisch würde ich für 12:30 Uhr reservieren. Damit wir nicht zu spät im Ferienlager ankommen, sollten wir spätestens 14 Uhr wieder losfahren, damit wir die letzten 20 km schaffen. Wir sind für 16:00 Uhr im Ferienlager angemeldet.“
Peter antwortet:
„Oh Gott, das kann sich doch niemand merken. Lass uns die Zeiten in einer Tabelle notieren:"
Ort
Uhrzeit
Entfernung von der Schule
Schule
9:00 Uhr
0 km
See
10:00 Uhr
Weiterfahrt
15 km
Restaurant
40km
Weiterfahrt
14:00 Uhr
Ferienlager
16:00 Uhr

Chris ruft von hinten:
„Zu viele Zahlen, können wir den Weg nicht aufzeichnen?
… Herr Friedrich, haben Sie eine Idee?“
Herr Friedrich: Versucht es doch einmal mit einem Koordinatensystem. Auf der x-Achse
beschriftet ihr die Uhrzeit, auf der y-Achse die zurückgelegte Strecke. Das könnte so aussehen:“
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
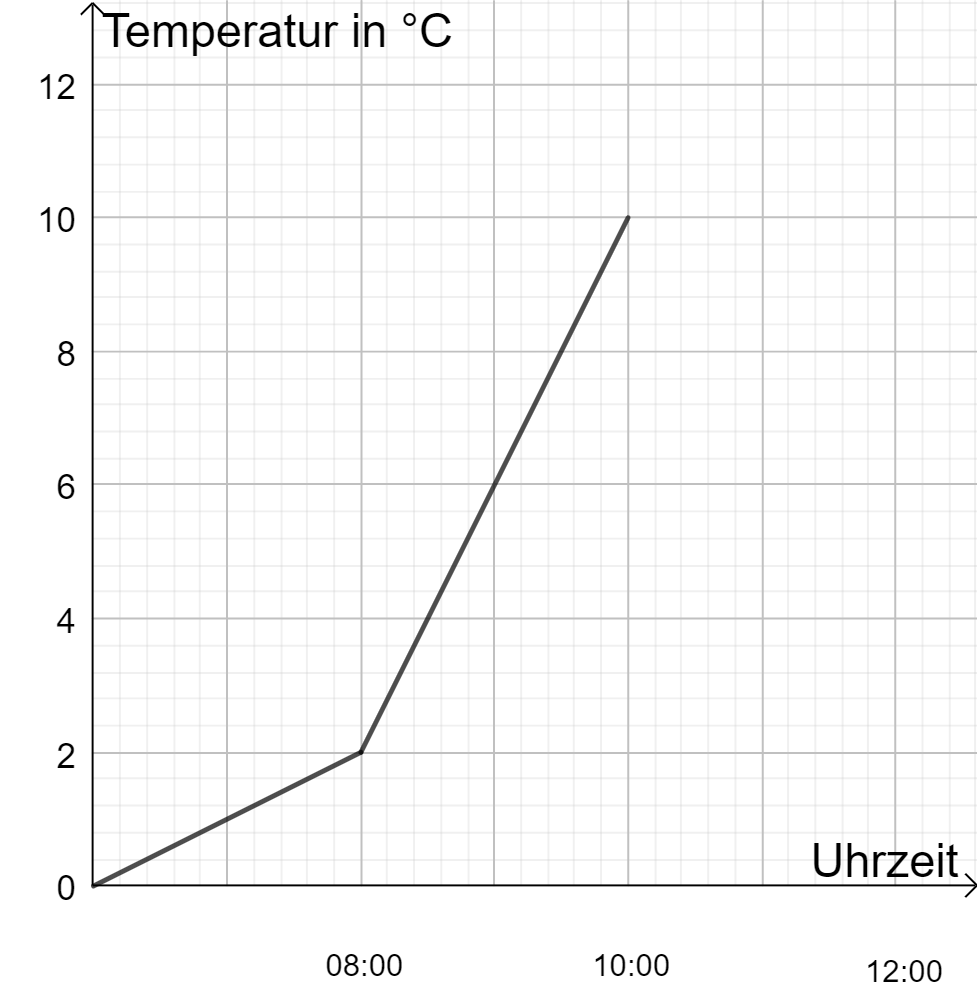
Zuordnungen können mit Hilfe verschiedener Darstellungsarten dargestellt werden. Beispiel: Uhrzeit → Temperatur
Text
Tabelle
Graph
Pfeile
Um 8:00 Uhr waren es 2°C, bis 10 Uhr stieg die Temperatur auf 10°C an.
Uhrzeit → Temperatur
Uhrzeit
Temperatur
8:00 Uhr
2° C
10:00 Uhr
10°C

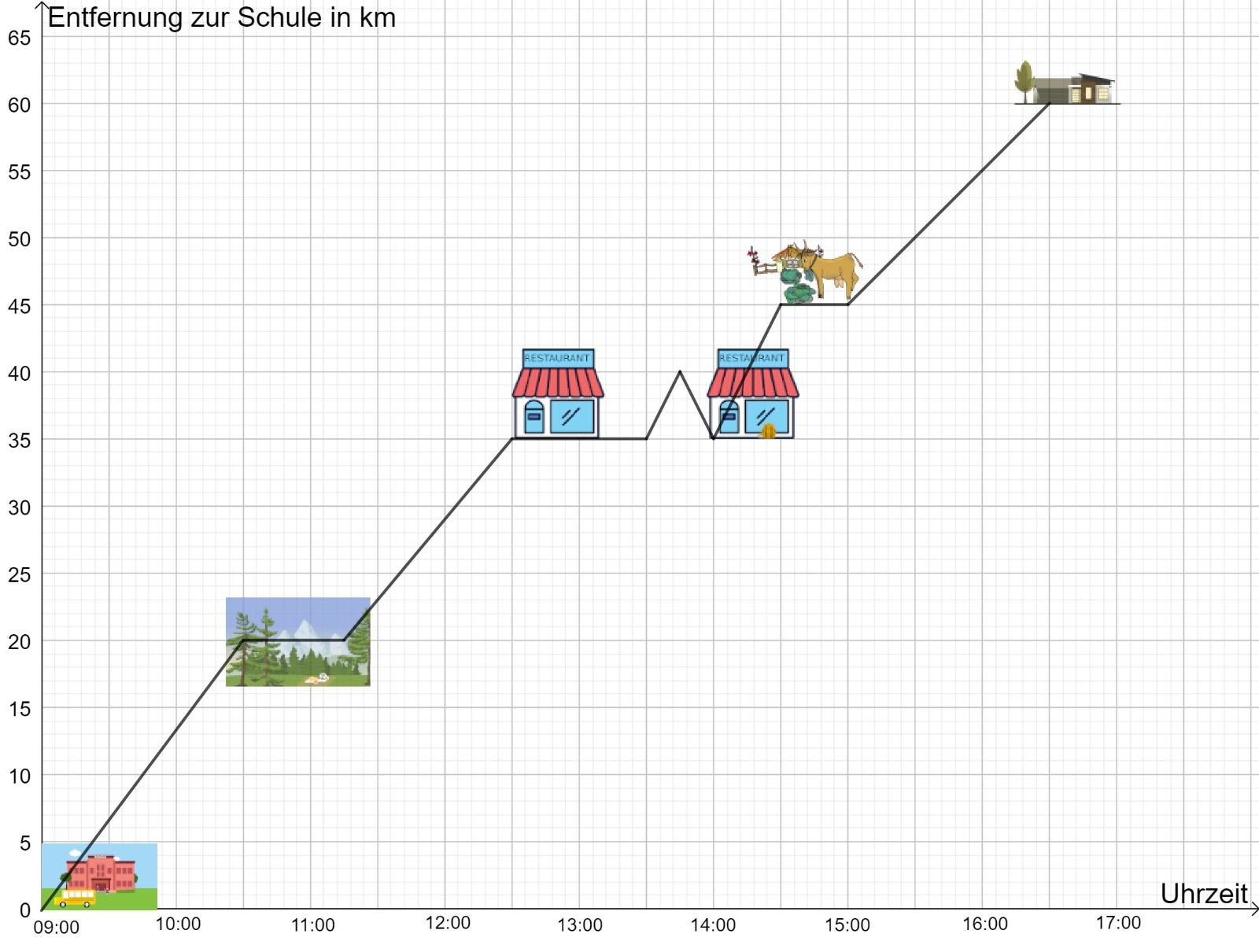
In der Unterkunft angekommen, warten alle auf die Gruppe 2. 16:30 Uhr kommen sie völlig erschöpft im Ferienlager an.
Um herauszufinden, warum die Gruppe 2 zu spät gekommen ist, zeichnet Greta den Fahrtweg ebenfalls mit Hilfe eines Koordinatensystems.
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
Partner-Experiment - Wie verändert sich dein Puls?
- Stoppuhr
- Kopiervorlage 3
du eine:n Arbeitspartner:in.
Jede:r von euch nimmt sich
eine eigene Kopiervorlage.
Vorbereitung
Durchführung
- Die erste Pulsmessung führst du im Sitzen durch (Ruhepuls).
Lege drei Finger (Zeige-, Mittel- und Ringfinger) auf die Arterie (Daumenseite) direkt unterhalb deines linken Handgelenkes.
Du spürst nun ein leichtes Klopfen – den Puls.
Zähle 30 Sekunden lang die Anzahl der Pulsschläge und multiplizieren den Wert mit 2. Notiere das Ergebnis. - Mache nun 5 Kniebeugen und miss erneut deinen Puls.
- Mache nun 15 Kniebeugen und miss erneut deinen Puls.
- Ruhe dich 5 Minuten aus und miss erneut deinen Puls.
- Mache nun 30 Kniebeugen und miss erneut deinen Puls.
Auswertung
- Übertrage jeweils die Werte in das Koordinatensystem und verbinde die Punkte einer Wertetabelle mit geraden Linien.
- Wer ist sportlicher? Beschreibe wie sich dein Puls und der Puls deines Partners / deiner Partnerin während der Übungen verändert hat. Wie könnte er sich während einer Sportstunde verändern? Begründe.
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
Check-out. Sammle mindestens 4 Sterne!

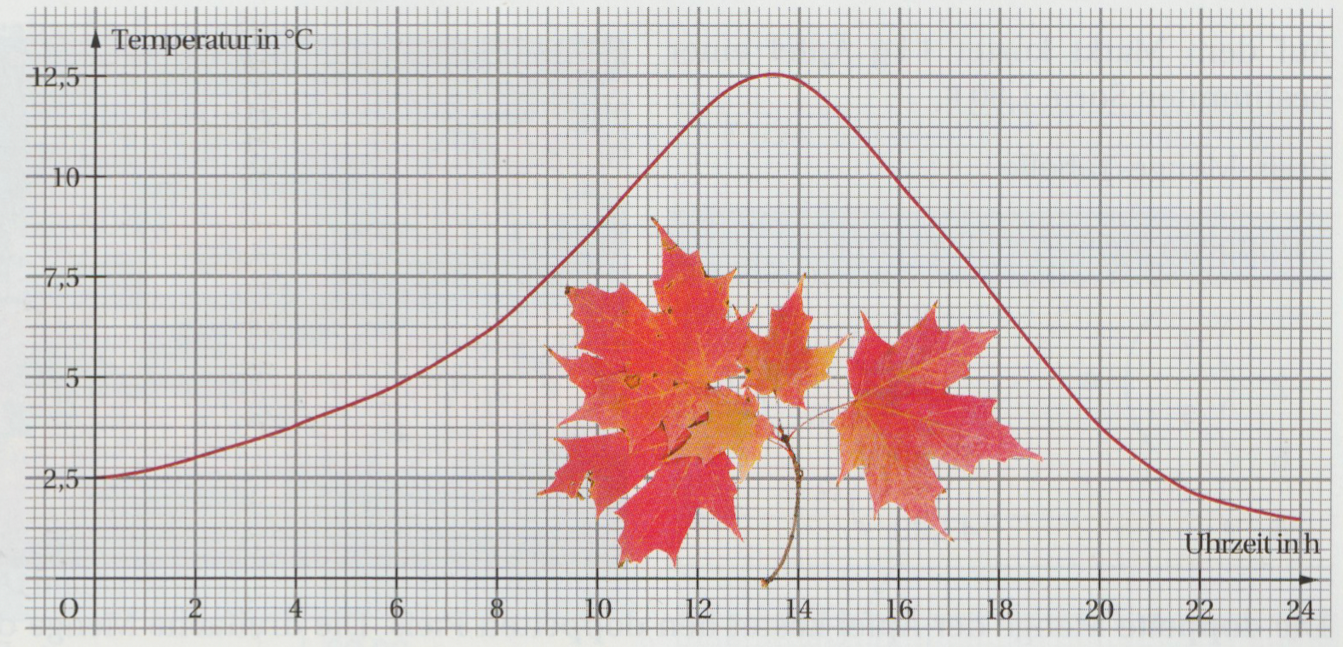
b) Beschreibe den Temperaturverlauf! In welcher Zeit stieg (fiel) die Temperatur am stärksten? Wann wurde die höchste Temperatur erreicht?
Uhrzeit in h
Temperatur
2
3 °C
4
...
24
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag

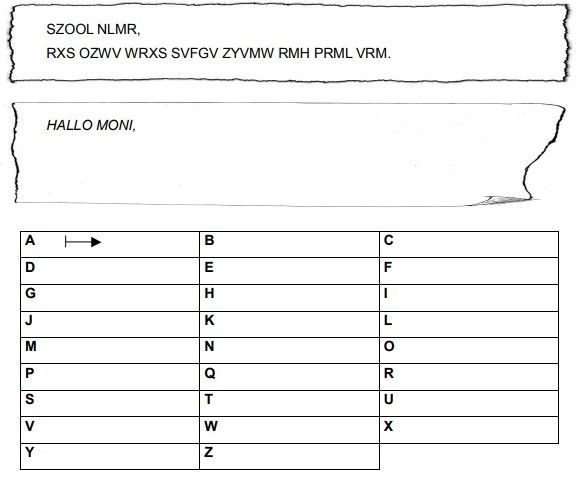
Z
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag

Tag
Do
Fr
Sa
So
Mo
Di
Mi
Do
Fr
Pegelstand in m
1,20
1,25
1,35
2,00
2,70
2,65
2,05
1,50
1,35


Finde zusammen. Schneide die Kärtchen der Kopiervorlage 4 aus und klebe die zusammengehörigen nebeneinander in dein Heft.

https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag
- (LINK) Eisoldt, J. (u.a.): Link Mathematik. Lehrbuch für die Klasse 6 Mittelschule Sachsen. Berlin: 2005, Duden Paetec GmbH
- (LIVE) mathe live 7. Ausgabe W: Schulbuch Klasse 7 (mathe live. Ausgabe W ab 2014). (2016). Klett.
- (SSS) Umstetter, H.: Spritztour, Schauspieler und Sommerurlaub. Den Zuordnungsbegriff kennenlernen. zuletzt abgerufen am 01.02.2022 unter: http://www.webhofmann.deresourcesZuordnungsbegriff.pdf
https://editor.mnweg.org/entdecken/dokument/zuordnungen-im-alltag


