Ich habe jetzt schon viel gelernt.
Aber ich kann noch mehr. Ich bin sicher, dass ich auch Winkel messen und Winkel zeichnen kann.
Du auch?
Komm, wir machen das zusammen!
Ich habe jetzt schon viel gelernt.
Aber ich kann noch mehr. Ich bin sicher, dass ich auch Winkel messen und Winkel zeichnen kann.
Du auch?
Komm, wir machen das zusammen!

Schau dir nochmal das Material zum Geodreieck aus Phase 5 an.
Meld dich beim Input an, wenn dir das schwer fällt.
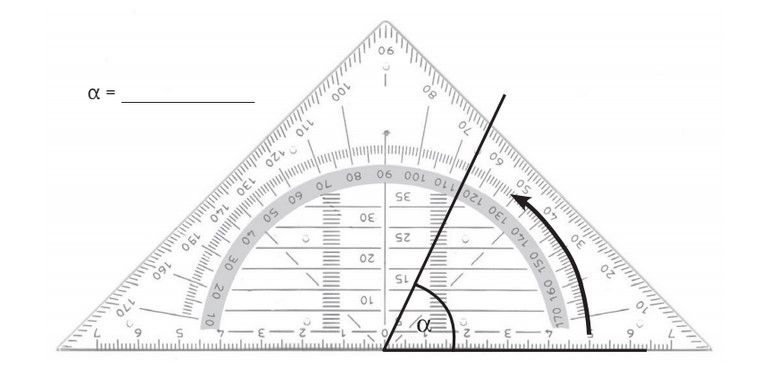
Denk an das Gradzeichen!
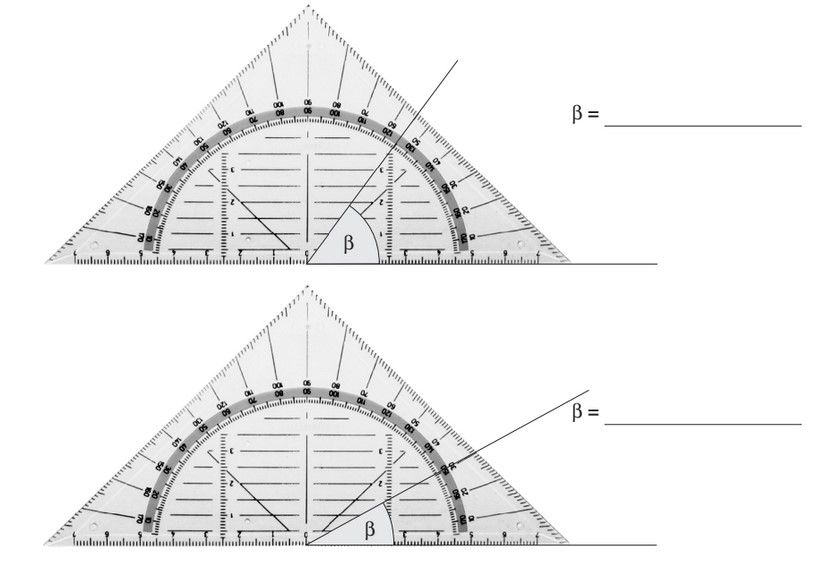
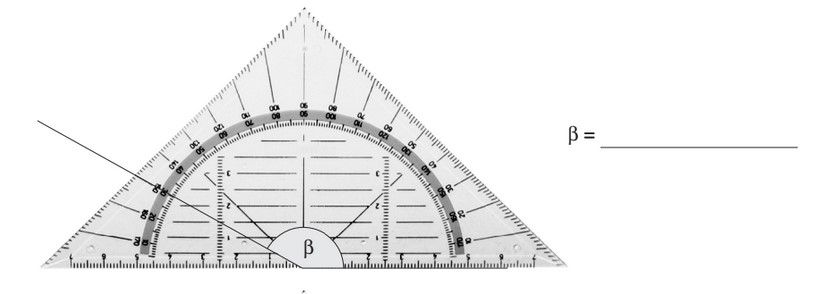
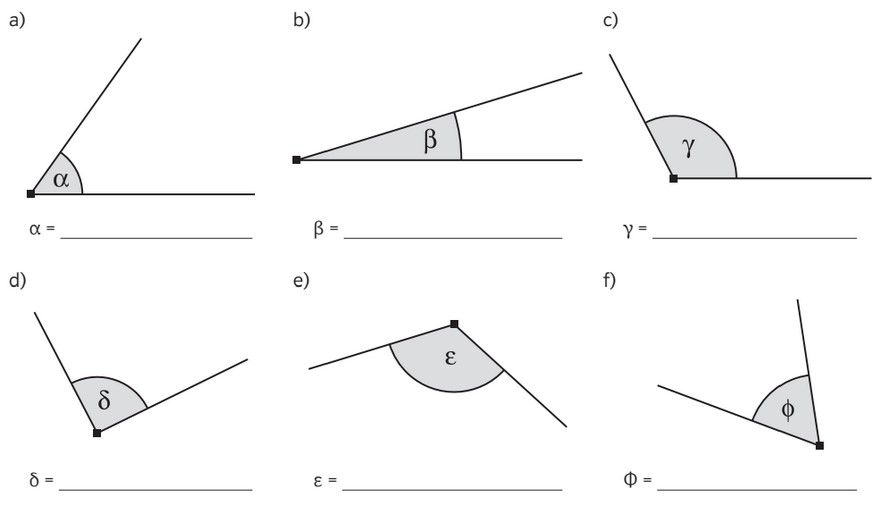
Du darfst die Schenkel verlängern, damit du das Winkelmaß besser ablesen kannst.
Du darfst das Blatt oder das Geodreieck drehen, damit du das Geodreeick besser anlegen kannst.
Für die nächsten Aufgaben brauchst du weißes Papier ohne Linien oder Karos! Wenn du das nicht hast, kannst du die Lernbegleitung im Lernbüro fragen.
Sie nutzen einen Browser mit dem mnweg.org nicht einwandfrei funktioniert. Bitte aktualisieren Sie Ihren Browser.
Sie verwenden eine ältere Version Ihres Browsers. Es ist möglich, dass mnweg.org mit dieser Version nicht einwandfrei funktioniert. Um mnweg.org optimal nutzen zu können, aktualisieren Sie bitte Ihren Browser oder installieren Sie einen dieser kostenlosen Browser: