Ein funk­ti­o­na­ler Zu­sam­men­hang be­schreibt, wie eine Grös­se (z. B. y) von einer an­de­ren Grös­se (z. B. x) ab­hängt. Ma­the­ma­tisch ge­se­hen ist das eine Zu­ord­nung, bei der jedem Wert von x genau ein Wert von y zu­ge­ord­net wird.



• Bei­spiel: Wenn du mit dem Fahr­rad fährst, hängt die zu­rück­ge­leg­te Stre­cke (y) von der Zeit (x) ab.

• Dar­stel­lung: Ta­bel­len, Gra­phen oder For­meln (z. B. y = 2x).

Ein Zu­sam­men­hang ist pro­por­ti­o­nal, wenn sich zwei Grös­sen im glei­chen Ver­hält­nis än­dern. Das be­deu­tet: Wenn x dop­pelt so gross wird, wird auch y dop­pelt so gross.



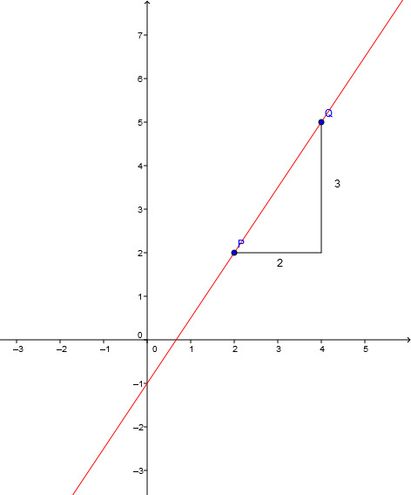
• Merk­mal: Ge­ra­de Linie durch den Ur­sprung im Ko­or­di­na­ten­sys­tem.

• For­mel: y = k · x (k ist die Pro­por­ti­o­na­li­täts­kon­stan­te).

• Bei­spiel: Wenn 1 Apfel 2 CHF kos­tet, kos­ten 3 Äpfel 6 CHF (y = 2 · x).

Ein Zu­sam­men­hang ist um­ge­kehrt pro­por­ti­o­nal, wenn das Pro­dukt der bei­den Grös­sen kon­stant bleibt. Wenn x grös­ser wird, wird y klei­ner – und um­ge­kehrt.



• Merk­mal: Hy­per­bel im Ko­or­di­na­ten­sys­tem.

• For­mel: x · y = k (k ist eine Kon­stan­te).

• Bei­spiel: Wenn 4 Ar­bei­ter 8 Tage für eine Ar­beit brau­chen, brau­chen 8 Ar­bei­ter nur 4 Tage (x · y = 32).

Funk­ti­o­na­le Zu­sam­men­hän­ge sind über­all im All­tag und in der Wis­sen­schaft. In Be­ru­fen wie Ar­chi­tek­tur, Wirt­schaft oder Tech­nik musst du Ab­hän­gig­kei­ten ver­ste­hen, um Pro­ble­me zu lösen:



• Pro­por­ti­o­na­li­tät: Beim Ein­kau­fen (Preis pro Ki­lo­gramm), beim Tan­ken (Kos­ten pro Liter Ben­zin) oder beim Um­rech­nen von Ein­hei­ten.

• Um­ge­kehr­te Pro­por­ti­o­na­li­tät: Bei der Pla­nung von Ar­beit (mehr Hel­fer = we­ni­ger Zeit) oder phy­si­ka­li­schen Ge­set­zen (z. B. Druck und Vo­lu­men bei Gasen).



Denk­fra­ge: Wie würde sich dein Ta­schen­geld än­dern, wenn du dop­pelt so viele Stun­den ar­bei­test?

1. Auf­ga­be: Ein Auto fährt mit kon­stan­ter Ge­schwin­dig­keit. In 2 Stun­den legt es 120 km zu­rück. Wie weit kommt es in 5 Stun­den?







Schritt 1: Finde k.

k = y / x = 120 km / 2 h = 60 km/h.



Schritt 2: Be­rech­ne y für x = 5 h.

y = k · x = 60 · 5 = 300 km.





Lö­sung: Das Auto fährt 300 km in 5 Stun­den.







2. Auf­ga­be: 6 Per­so­nen brau­chen 12 Stun­den, um einen Zaun zu bauen. Wie lange brau­chen 9 Per­so­nen?





Schritt 1: Finde k.

k = x · y = 6 · 12 = 72.



Schritt 2: Be­rech­ne y für x = 9.

y = k / x = 72 / 9 = 8 Stun­den.







Lö­sung: 9 Per­so­nen brau­chen 8 Stun­den.

Pro­por­ti­o­na­li­tät

1. Ein Kilo Äpfel kos­tet 3 CHF. Wie viel kos­ten 4 kg Äpfel?

2. Ein Zug fährt 150 km in 3 Stun­den. Wie weit fährt er in 7 Stun­den?

3. Für 5 Meter Stoff zahlst du 20 CHF. Wie viel kos­tet 12 Meter Stoff?



Um­ge­kehr­te Pro­por­ti­o­na­li­tät

1. 8 Ar­bei­ter bauen ein Haus in 10 Tagen. Wie lange brau­chen 5 Ar­bei­ter?

2. Ein Auto fährt mit 60 Li­tern Ben­zin 480 km. Wie weit kommt es mit 40 Li­tern?

3. Ma­schi­nen pro­du­zie­ren 120 Teile in 4 Stun­den. Wie lange brau­chen 6 Ma­schi­nen?



Ge­misch­te Auf­ga­ben

1. Ein Re­zept für 4 Per­so­nen braucht 200 g Mehl. Wie viel Mehl brauchst du für 10 Per­so­nen? (Pro­por­ti­o­na­li­tät)

2. 12 Schü­ler tei­len sich einen Ku­chen in 6 Mi­nu­ten. Wie lange brau­chen 8 Schü­ler? (Um­ge­kehr­te Pro­por­ti­o­na­li­tät)

3. Zeich­ne den Gra­phen für y = 3x (Pro­por­ti­o­na­li­tät) und über­prü­fe mit 3 Wer­te­paa­ren.

4. Über­le­ge: Wenn du dop­pelt so schnell fährst, wie lange brauchst du dann für eine Stre­cke? (Um­ge­kehr­te Pro­por­ti­o­na­li­tät)