Die folgenden Aufgaben zeigen exemplarisch, wie das Thema in der Abiturprüfung abgefragt werden kann. Die Aufgaben 1 bis 3 stammen aus dem Pflichtteil. Für die Lösung der Aufgaben sind keine Hilfsmittel zugelassen.

1

Gegeben sind die Geraden

g : x = 3 - 3 3 + r \cdot 34 - 1

und

h : x = 3 - 3 3 + s \cdot 5 - 3 3

mit

r, s ϵ R

.

a) (1) Geben Sie die Koordinaten des Schnittpunkts von

g

und

h

an.
(2) Zeigen Sie, dass

g

und

h

senkrecht zueinander verlaufen.

b) Die Ebene

E

enthält die Geraden

g

und

h

. Bestimmen Sie eine Gleichung von

E

in Koordinatenform.

(Konvolut Leistungsfach Mathematik ab 2023, Baden-Württemberg)

2

Gegeben ist die Ebene

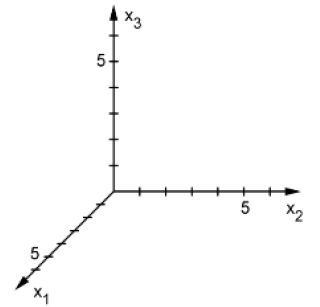
E : x_{1} + x_{2} + 2 x_{3} = 24

und die Gerade

g : x = 21 - 2 + t \cdot 2 - 1 - 3

mit

t ϵ R

.

a) Zeichnen Sie in die Abbildung die Schnittgerade von

E

mit der

x_{2} x_{3}

-Ebene ein.

b) Berechnen Sie die Koordinaten des Schnittpunkts von

E

und

g

.

(Konvolut Leistungskurs Mathematik Abitur 2021, Baden-Württemberg)

3

Gegeben ist die Ebene

E : 2 x_{1} + x_{2} - 2 x_{3} = - 18

.

a) Der Schnittpunkt von

E

mit der

x_{1}

-Achse, der Schnittpunkt von

E

mit der

x_{2}

-Achse und der Koordinatenursprung sind die Eckpunkte eines Dreiecks. Bestimmen Sie den Flächeninhalt dieses Dreiecks.

b) Ermitteln Sie die Koordinaten des Vektors, der sowohl ein Normalenvektor von

E

als auch der Ortsvektor eines Punkts der Ebene ist.

(Konvolut Leistungskurs Mathematik Abitur 2021, Baden-Württemberg)

Für die Aufgaben 4 bis 7 darf ein Taschenrechner und die mathematische Merkhilfe für die Abiturprüfung in Baden Württemberg benutzt werden.

Du findest sie hier:

4

Gegeben ist der Punkt

R (4∣ -2 ∣4)

und die Ebenenschar

E_{k} : k x_{1} + k x_{2} + x_{3} = 14

mit

k ϵ R

.

a) (1) Beschreiben Sie die besondere Lage der Ebene

E_{0}

im Koordinatensystem.
(2) Bestimmen Sie diejenige Schar, die den Punkt

R

enthält.
(3) Zeigen Sie, dass es eine Gerade

g

gibt, die in allen Ebenen der Schar liegt.

b) Gegeben sind die Spurpunkte

S_{1} (7∣0∣0)

,

S_{2} (0∣7∣0)

und

S_{3} (0∣0∣14)

einer Ebene

E

.
(1) Begründen Sie, dass die Ebene

E

eine Ebene der Schar ist.
(2) Betrachtet wird ein gerader Kegel mit der Spitze

S_{3}

, dessen Grundkreis in der

x_{1} x_{2}

-Ebene liegt. Die Punkte

S_{1}

und

S_{2}

liegen auf dem Grundkreis. Untersuchen Sie, ob der Punkt

R

innerhalb des Kegels liegt.
(3) Bestimmen Sie eine Koordinatengleichung der Ebene, die den Kegel in der Strecke

\overline{S_{1} S_{3}}

berührt.

(Konvolut Leistungskurs Mathematik Abitur 2021, Baden-Württemberg)

5

Gegeben sind die Punkte

A (6∣1∣0)

,

B (4∣5∣ - 4)

und

C (- 2∣8∣2)

.
(1) Zeigen Sie, dass das Dreieck

A BC

bei

B

einen rechten Winkel besitzt.
(2) Die drei Punkte liegen in einer Ebene

E

. Bestimmen Sie die Koordinatengleichung von

E

.
(3) Es gibt einen Punkt

D

, für den das Viereck

A BC D

ein Rechteck ist. Ermitteln Sie die Koordinaten von

D

.

(Konvolut Leistungskurs Mathematik Abitur 2021, Baden-Württemberg)

6

Zwei Schülerinnen lösen dasselbe lineare Gleichungssystem. Sie erhalten die Lösungsmengen

L_{1} = {(2 - r; 1 + r; 3 - r) ∣ rϵ R}

bzw.

L_{2} = {(1 - s; - s; 4 + s) ∣ sϵ R}

.
Untersuchen Sie, ob diese Lösungsmengen identisch sind.

(Konvolut Leistungskurs Mathematik Abitur 2021, Baden-Württemberg)

7

Gegeben ist die Ebenenschar

E_{k} : 3 x_{1} + k x_{2} - k x_{3} = 6

(

k ϵ R

) sowie die Gerade

g

durch die Punkte

P (4∣7∣7)

und

Q (1∣2∣9)

.

a) Untersuchen Sie die Ebenen

E_{k}

der Schar auf Parallelität zur Geraden

g

und Orthogonalität zur Geraden

g

.

b) (1) Bestimmen Sie

k

so, dass

E_{k}

orthogonal zu

E_{1}

ist.
(2) Untersuchen Sie, ob es eine Ebene

E_{k}

gibt, die zu keiner anderen Ebene der Schar orthogonal ist.

c) (1) Zeigen Sie, dass es eine Gerade

h

gibt, die in allen Ebenen

E_{k}

liegt.
(2) Ermitteln Sie die Gleichung einer Ebene

F

, die

h

enthält, aber nicht zur Ebenenschar

E_{k}

gehört.

d) Untersuchen Sie, welche Punkte der

x_{2} x_{3}

-Ebene in keiner Ebene

E_{k}

liegen.

(Konvolut Leistungskurs Mathematik Abitur 2021, Baden-Württemberg)

Lösungen

1. a1) $S (3∣ - 3∣3)$

a2) Nachweis mithilfe des Skalarproduktes:

$34 - 1 \cdot 5 - 3 3 = 15 - 12 - 3 = 0$

b) $E : 9 x_{1} - 14 x_{2} - 29 x_{3} = - 18$

3. a) Schnittpunkte von $E$ mit der $x_{1}$ und $x_{2}$ -Achse: $S_{1} (- 9∣0∣0)$ und $S_{2} (0∣ - 18∣0)$

Flächeninhalt: $A = 0, 5 \cdot 9 \cdot 18 = 81$

b) Für jeden Normalenvektor von $E$ gilt: $n = 2 r r - 2 r$ mit $r ϵ R \ {0}$

$2 \cdot 2 r + r - 2 \cdot (- 2 r) = - 18 \Rightarrow r = - 2$

$n = - 4 - 2 4$

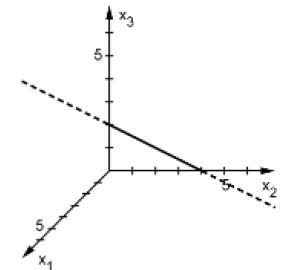
2. a)

b) $S (0∣2∣1)$

Lösungen

4. a1) Die Ebene $E_{0}$ ist parallel zur $x_{1} x_{2}$ -Ebene.

a2) Eine Punktprobe von $R$ in $E_{k}$ führt zu der Gleichung $4 k - 2 k + 4 = 14$ mit der Lösung

$k = 5$ . Die Ebene $E_{5}$ enthält den Punkt $R$ .

a3) Die Gerade wird ermittelt, indem die Schnittgerade zweier beliebiger Ebenen der Ebenenschar bestimmt wird. Der Schnitt von $E_{0}$ und $E_{1}$ führt zum LGS

$I . I I . 1 x_{1} + 1 x_{2} + 1 x_{3} 1 x_{3} = = 1414$

mit der Lösungsmenge $L = {t; - t, 14}$ .

Daraus lässt sich die Gerade $g$ aufstellen:

$g : x = x_{1} x_{2} x_{3} = t - t 14 = 0 + 1 t 0 - 1 t 14 + 0 t = 0014 + t \cdot 1 - 1 0$

Die Gerade $g$ liegt in jeder Ebene der Schar, da für jedes $k ϵ R$ und jedes $t ϵ R$ eine wahre Aussage entsteht:

$k \cdot (0 + t) + k \cdot (0 - t) + 14 = 14$

$14 = 14 ✓$

b1) Punktprobe $S_{1} ϵ E_{k}$ liefert $k = 2$ . Punktproben ergeben, dass $S_{2}$ und $S_{3}$ ebenfalls in der Ebene $E_{2}$ liegen.

b2) Aus den Spurpunkten ergibt sich, dass der Grundkreis den Mittelpunkt $O (0∣0∣0)$ und den Radius $r = 7$ hat. Durch die Punkte $S_{3}$ und $R$ wird eine Hilfsgerade aufgestellt:

$g : x = 0014 + t \cdot 4 - 2 - 10$

Nun wird geprüft, ob der Spurpunkt der Hilfsgeraden in der $x_{1} x_{2}$ -Ebene innerhalb des Grundkreises liegt. Als Spurpunkt ergibt sich $P (5, 6∣ - 2, 8∣0)$ . Der Abstand zum Mittelpunkt ist $∣ OP ∣ = 5, 6^{2} + (- 2, 8)^{2} + 0^{2} \approx 6, 62$

Da $6, 62 < r$ liegt $P$ innerhalb des Grundkreises und somit der Punkt $R$ innerhalb des Kegels.

Lösungen

b3) Die gesuchte Ebene $F$ enthält die Punkte $S_{1}$ und $S_{3}$ und ist parallel zur $x_{2}$ -Achse. Der Normalenvektor $n$ lässt sich als Vektorprodukt der Vektoren $S_{1} S_{3}$ und einem Vektor, der in

$x_{2}$ -Richtung zeigt, bestimmen:

$- 1 02 \times 010 = - 2 0 - 1$

Mit dem Normalenvektor und dem Punkt $S_{3}$ ergibt sich die Ebenengleichung:

$F : 2 x_{1} + x_{3} = 14$

5. (1) $B A \cdot BC = 2 - 4 4 \cdot - 6 36 = 0$

(2) $E : 2 x_{1} + 2 x_{2} + x_{3} = 14$

(3) $d = a + BC = 046$ ; $D (0∣4∣6)$

6. Die beiden Lösungsmengen lassen sich als Geraden interpretieren:

$g : x = 213 + t \cdot 11 - 1$

Die Untersuchung der Geraden zeigt, dass diese identisch sind. Somit sind auch die Lösungsmengen identisch.

Lösungen

7. a) Untersuchung auf Parallelität

Normalenvektor der Ebenenschar:

$n = 3 k - k$

Wenn die Ebene und die Gerade parallel zueinander sind, müssen der Normalenvektor der Ebene und der Richtungsvektor der Geraden senkrecht zueinander sein, also ein Skalarprodukt haben, das null ist.

$n \cdot PQ = 3 k - k \cdot - 3 - 5 2 = 0$

$- 9 - 5 k - 2 k = 0$

$k = - \frac{9}{7}$

Die Ebene $E_{- \frac{9}{7}}$ und die Gerade $g$ sind parallel zueinander.

Untersuchung auf Orthogonalität

Die Gerade und die Ebene sind orthogonal zueinander, wenn der Normalenvektor der Ebene und der Richtungsvektor der Geraden linear abhängig sind:

$r \cdot n = PQ$

$r \cdot 3 k - k = - 3 - 5 2$

$I . I I . I I I . 3 r r k - r k = = = -3 \Rightarrow r = - 1 - 5 \Rightarrow k = 5 2 \Rightarrow k = 2$

Da sich für $k$ unterschiedliche Werte ergeben, gibt es einen Widerspruch. Keine Ebene der Ebenenschar $E_{k}$ ist orthogonal zu $g$ .

Richtungsvektor der Geraden:

$PQ = - 3 - 5 2$

Lösungen

7. b1) $E_{1} : 3 x_{1} + 1 x_{2} - 1 x_{3} = 6$

$n_{1} \cdot n_{k} = 31 - 1 \cdot 3 k - k = 0 \Rightarrow k = - \frac{9}{2}$

Die Ebene $E_{- \frac{9}{2}}$ ist orthogonal zu $E_{1}$ .

b2) $n_{k}_{1} \cdot n_{k}_{2} = 3 k_{1} - k_{1} \cdot 3 k_{2} - k_{2} = 0 \Rightarrow 9 + 2 k_{1} k_{2} = 0$

Für $k_{1} = 0$ ergibt sich für die Gleichung $9 + 2 k_{1} k_{2} = 0$ ein Widerspruch. Somit ist die Ebene $E_{0}$ zu keiner anderen Ebene der Schar orthogonal.

c1) Für die Schnittgerade der Ebenen $E_{0}$ und $E_{1}$ ergibt sich:

$h : x = 200 + t \cdot 011$

Die Schnittgerade wird in die Ebenenschar eingesetzt:

$3 \cdot 2 + k \cdot t - k \cdot t = 6$

$6 = 6 ✓$

Es entsteht eine wahre Aussage, die Schnittgerade liegt in allen Ebenen der Schar.

c2) Alle Ebenen, die die Gerade $h$ enthalten, enthalten den Punkt $R (2∣0∣0)$ . Darüber hinaus ist ihr Normalenvektor senkrecht zum Richtungsvektor der Geraden. Alle Vektoren der Form

$n = a k - k$ erfüllen diese Bedingung. In der Ebenenschar $E_{k}$ ist $a = 3$ . Somit muss für den Normalenvektor der Ebene $F$ gelten: $a \neq = 3$ . Eine mögliche Lösung ist:

$F : x - 200 \cdot 01 - 1 = 0$

Hinweis

Da der Nullvektor kein Normalenvektor sein kann, dürfen $a$ und $k$ nicht beide null sein.

Lösungen

7. d) Für alle Punkte der $x_{2} x_{3}$ -Ebene gilt: $S (0∣ x_{2} ∣ x_{3})$ . Mit diesem Punkt wird eine Punktprobe durchgeführt:

$3 \cdot 0 + k x_{2} - k x_{3} = 6$

$k x_{2} - k x_{3} = 6$

$k \cdot (x_{2} - x_{3}) = 6$

Für $x_{2} = x_{3}$ hat diese Gleichung keine Lösung.

Somit sind die Punkte, die in keiner Ebene der Schar liegen, alle Punkte für die gilt: $S (0∣ x_{2} ∣ x_{2})$ mit $x_{2} ϵ R$ .