Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
GN
Aufgaben aus dem Abitur
Mathematik Gleichungen
Die folgenden Aufgaben zeigen exemplarisch, wie das Thema in der Abiturprüfung abgefragt werden kann. Sie stammen alle aus dem Pflichtteil. Für die Lösung der Aufgaben sind somit keine Hilfsmittel zugelassen.
1
Bestimmen Sie die Lösungsmenge des LGS.
a)
I. II. III. x13x1 x1+−− 2x2 1x2 5x2++− 3x3 2x3 4x3=== 14 7 -21
b)
I. II. III. 3x15x1 x1−−+ 2x2 4x2 3x2+−− x3 x3 2x3=== 2r 2 2r+6
(Konvolut Leistungsfach Mathematik ab 2023, Baden-Württemberg)
2
Bestimmen Sie für r ϵ R die Lösungsmenge des linearen Gleichungssystems.
I. II. III. 2x14x12x1−++ 2x2 x2 3x2+−− x3 3x3 3x3=== 6 4r 8r
(Konvolut Leistungsfach Mathematik 2021 und 2022, Baden-Württemberg)
3
Der Graph einer ganzrationalen Funktion f dritten Grades hat im Ursprung einen Hochpunkt und an der Stelle x = 2 die Tangente mit der Gleichung y = 4x – 12. Bestimmen Sie eine Funktionsgleichung von f.
(Prüfungsaufgaben Abitur Mathematik 2015, Baden-Württemberg)
4
Für eine ganzrationale Funktion h zweiten Grades gilt: T (-1|-4) ist Tiefpunkt und Q (2|5) ein weiterer Punkt ihres Schaubilds. Ermitteln Sie eine Funktionsgleichung von h.
(Prüfungsaufgaben Abitur Mathematik 2008, Baden-Württemberg)
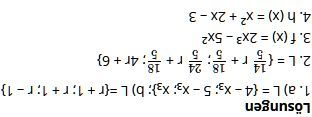
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/aufgaben-aus-dem-abitur-3
https://editor.mnweg.org/mnw/dokument/aufgaben-aus-dem-abitur-3


