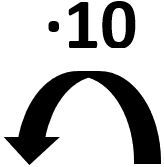
Das bei uns gebräuchliche Zahlensystem wird Dezimalsystem [von lateinisch „decimus“ Zehnter] genannt. Es enthält die zehn verschiedenen Ziffern 0 bis 9. Um in der Stellenwerttafel eine Stufe nach oben zu gelangen, muss mit zehn multipliziert werden.

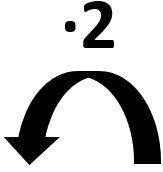
So ähnlich ist es beim Dualsystem, das auch Zweiersystem oder Binärsystem genannt wird. Es kommt mit nur zwei Zeichen aus, nämlich 0 und 1. Wie das Dezimalsystem ist es ein Stellenwertsystem. Dabei ist die Umrechnungszahl 2.

Ein Beispiel für eine Zahl im Dualsystem ist 10011₂ . Die tiefgestellte „2“ deutet darauf hin, dass die Zahl im Dualsystem steht. Manchmal wird statt der „1“ auch ein senkrechter Strich geschrieben, um zu verdeutlichen, dass eine Zahl im Dualsystem steht: I00I0. Um die Zahl ins Dezimalsystem umzurechnen, wird sie in die Stellenwerttafel eingetragen:

Nun werden alle Zahlen addiert, bei denen eine „1“ steht: 16 + 2 + 1 = 19.

10011₂ = 19

Um eine Zahl vom Dezimalsystem ins Dualsystem umzurechnen, wird eine Wertetabelle genutzt. Dabei wird zuerst die größtmögliche Zahl gesucht, die in die umzurechnende Zahl hineinpasst.

Bei der Zahl 22 ist das die 16. In dieses Feld wird eine „1“ eingetragen. Wie beim Dezimalsystem bleiben die Felder links von dem ersten Feld, in das etwas eingetragen wird, leer.

Nun wird geschaut, wie groß der Rest ist: 22 – 16 = 6. Für den Rest wird wieder geprüft, welches die größtmögliche Zahl in der Stellenwerttafel ist, die in die Zahl hineinpasst. Das ist nun die 4. Dort wird wieder eine „1“ eingetragen. In alle Lücken davor kommt eine „0“.

Erneut wird der Rest bestimmt: 6 – 4 = 2. Die 2 kommt direkt in der Stellenwerttafel vor. Dort wird eine „1“ eingetragen. Weil es keinen weiteren Rest gibt, kommt in alle anderen Felder dahinter eine „0“.

Damit ist die Umrechnung fertig. Die Probe zeigt: 16 + 4 + 2 = 22. Daher gilt: 22 = 10110₂.