TitelDas Vektorprodukt
AutorMNWeG
veröffentlicht04.02.2022
FachMathematik
KompetenzbereichVektoren
Phase12
MaterialformInputmaterial

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Arbeitsauftrag

Erarbeite dir die Rechenregeln zum Vektorprodukt, indem du die Aufgaben löst. Wenn du nicht weiter kommst, findest du die Lösungen am Ende des Dokuments.

Was ist ein Vektorprodukt?

Das Vektorprodukt, das auch Kreuzprodukt genannt wird, ist eine mathematische Verknüpfung von zwei Vektoren. Dabei werden die Koordinaten der beteiligten Vektoren in einem Kreuzmuster multipliziert und anschließend subtrahiert. Das Ergebnis einer Vektormultiplikation ist im Vergleich zur Skalarmultiplikation ein Vektor. Das Rechenzeichen für das Vektorprodukt ist ein Kreuz $\times$ .

Wie wird ein Vektorprodukt berechnet?

Die Formel für die Berechnung des Vektorproduktes von Vektoren lautet:

$a \times b = a_{1} a_{2} a_{3} \times b_{1} b_{2} b_{3} = a_{2} b_{3} - a_{3} b_{2} a_{3} b_{1} - a_{1} b_{3} a_{1} b_{2} - a_{2} b_{1}$

Vektorprodukte können nur für Vektoren mit drei Koordinaten berechnet werden. Eine Berechnung des Vektorproduktes für einen Vektor mit zwei Koordinaten ist nicht möglich.

Beispiel

$a = 136$ , $b = - 1 - 2 5$

$a \times b = 136 \times - 1 - 2 5 = 3 \cdot 5 - 6 \cdot (- 2) 6 \cdot (- 1) - 1 \cdot 5 1 \cdot (- 2) - 3 \cdot (- 1)$

$a \times b = 27 - 11 1$

Schau dir die Formel zur Berechnung des Vektorproduktes genau an. Gib eine mögliche Begründung an, warum das Vektorprodukt von Vektoren mit zwei Koordinaten nicht berechnet werden kann.

Rechentrick: Das Vektorprodukt schnell und einfach berechnen

Die Formel für das Vektorprodukt sieht auf den ersten Blick etwas kompliziert aus. Mit den folgenden Schritten lässt sich das Vektorprodukt dennoch schnell und einfach berechnen.

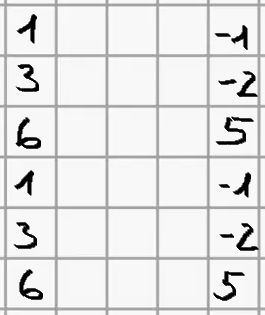
$136 \times - 1 - 2 5$

(1) Schreibe beide Vektoren

ohne Klammern jeweils

zweimal untereinander.

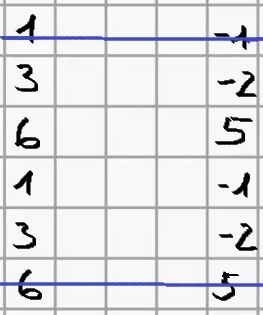
(2) Streiche die obere

und die untere Zeile durch.

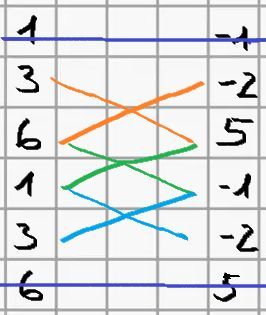
(3) Verbinde nun die restlichen

Zahlen mit drei Kreuzen.

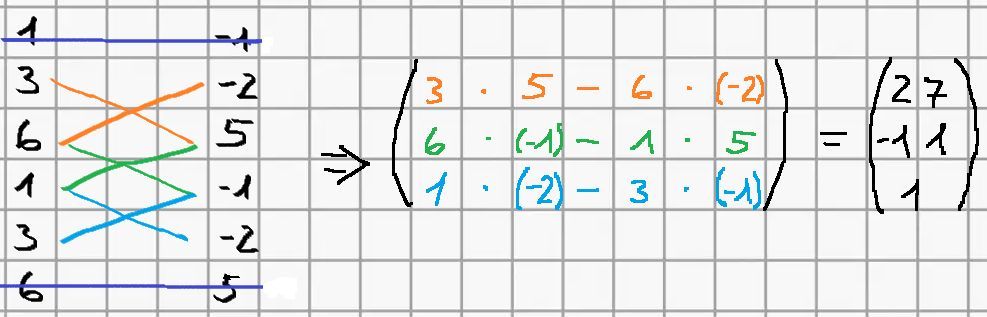
(4) Jedes Kreuz steht für eine Zeile im Vektor, die berechnet wird. Multipliziere die verbundenen Zahlen miteinander. Ziehe dann in jeder Zeile das zweite Produkt vom ersten Produkt ab.

Die geometrische Bedeutung des Vektorproduktes

Im Beispiel oben wurde das Vektorprodukt der Vektoren $a$ und $b$ berechnet. Das Vektorprodukt soll ab nun $n$ heißen.

$a = 136$ , $b = - 1 - 2 5$ , $a \times b = n = 27 - 11 1$

a) Berechne die Skalarprodukte von

a

und

b

mit

n

b) Wenn du dich nicht verrechnet hast, sollten die Ergebnisse gleich sein und eine Besonderheit aufweisen. Beschreibe die Besonderheit.

c) Ergänze den Merksatz zur geometrischen Bedeutung des Vektorproduktes.

Bei der Vektormultiplikation entsteht ein Vektor, der senkrecht auf den beiden beteiligten Vektoren steht.

Lösung

Aufgabe 1

Bei der Berechnung des Vektorproduktes werden in jeder Zeile die Werte aus den anderen beiden Zeilen benötigt. In einem Vektor mit nur zwei Zeilen wäre eine solche Berechnung nicht möglich, da immer eine Zeile fehlen würde.

Aufgabe 2

b) In beiden Fällen ist das Skalarprodukt null.

c) Bei der Vektormultiplikation entsteht ein Vektor, der senkrecht auf den beiden beteiligten Vektoren steht.

$a \cdot n = 136 \cdot 27 - 11 1 = 0$

$b \cdot n = - 1 - 2 5 \cdot 27 - 11 1 = 0$