Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Diagrammarten
Diese Diagrammarten solltest du kennen und auch zeichnen können:
- Balkendiagramm
- Säulendiagramm
- Streifendiagramm
- Kreisdiagramm
- Liniendiagramm
- Piktogramm/Bilddiagramm
1
Schaue dir die beiden Diagramme genau an. Dargestellt wird die Entwicklung des Preisindexes in Baden-Württemberg. Preisindex steht für Preissteigerung in %, bezogen auf das Jahr 2020, bei dem 100 % angesetzt werden. Vor 2020 sind die Zahlen also kleiner 100 %, danach größer.
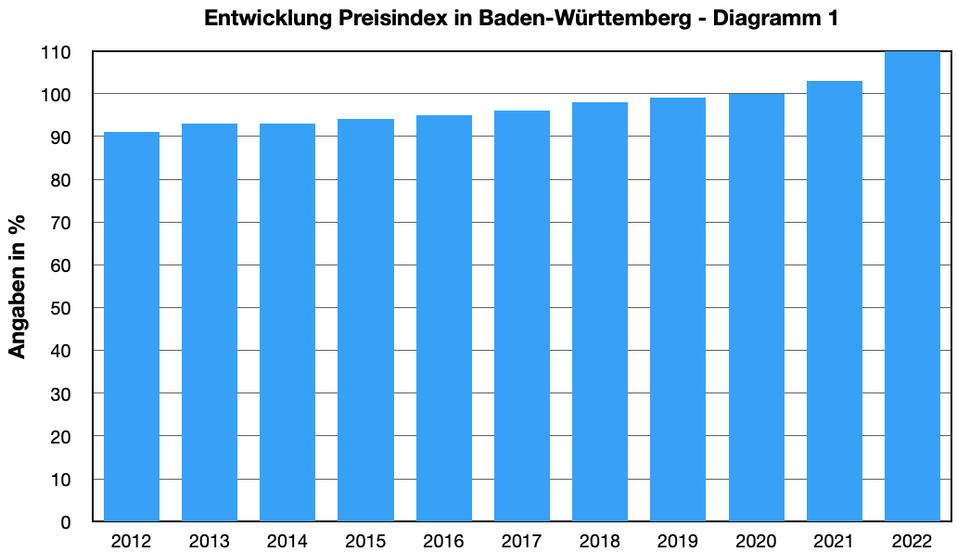
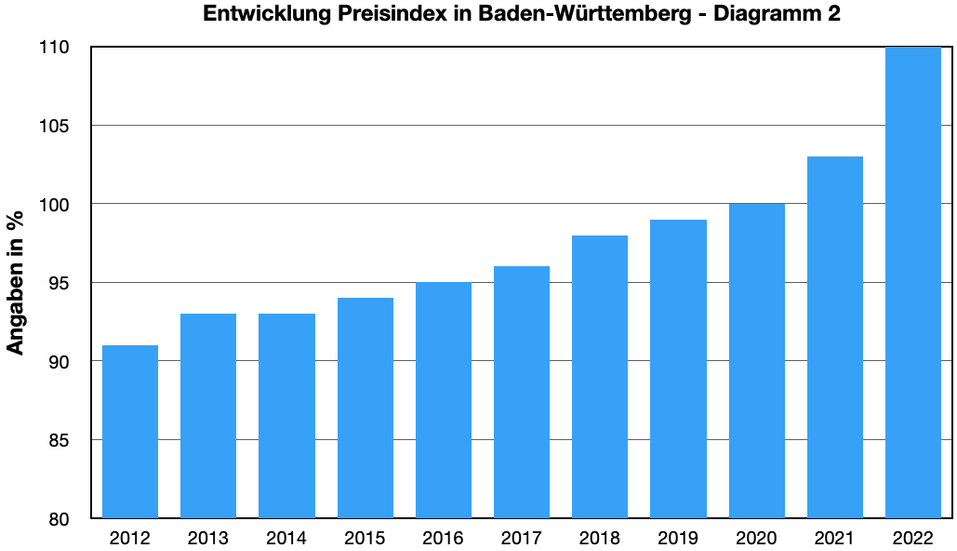
- Schreibe auf, was dir auffällt, wenn du die Diagramme vergleichst. Es gibt genau einen
entscheidenden Unterschied. Wie wirkt sich dieser Unterschied aus? - Um wie viel Prozent sind die Preise zwischen 2012 und 2022 gestiegen?
- In welchen Jahren sind die Preise schneller gestiegen?
2
In diesem Säulendiagramm siehst du die
monatlichen Anmeldezahlen für einen
Deutschkurs in Tiengen.
monatlichen Anmeldezahlen für einen
Deutschkurs in Tiengen.
- Wie viele Personen haben in dem
abgebildeten Zeitraum insgesamt an
den Kursen teilgenommen? - Zwischen welchen zwei aufeinander
folgenden Monaten war der geringste
Unterschied zwischen den Anmeldezahlen? - Wie groß ist der prozentuale Unterschied von dem Monat mit den höchsten zu dem Monat mit den niedrigsten Anmeldezahlen?
Anmeldezahlen für Deutschkurse in Tiengen
3
In dem Kreisdiagramm siehst du die
AG-Angebote einer Schule und die
prozentuale Verteilung der LPs auf die
einzelnen AGs. Insgesamt nahmen 250 LPs teil.
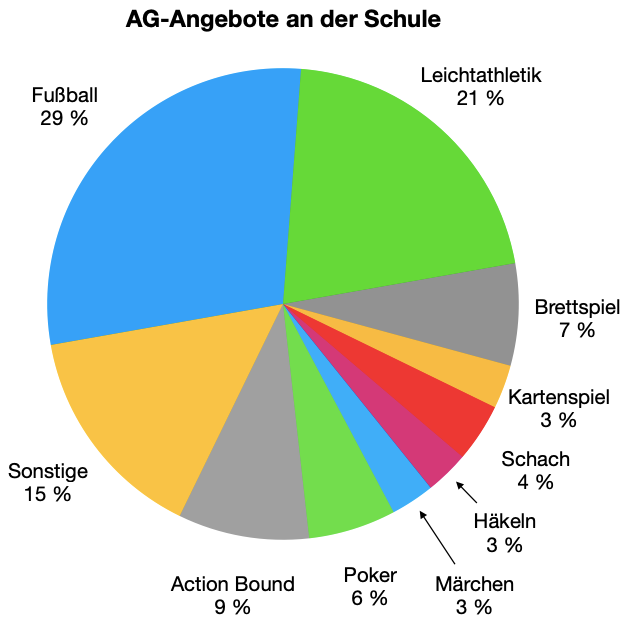
AG-Angebote einer Schule und die
prozentuale Verteilung der LPs auf die
einzelnen AGs. Insgesamt nahmen 250 LPs teil.
- Wie viele LPs nahmen an der
Brettspiel AG teil? - Wie viele LPs nahmen an den AGs
Fußball und Leichtathletik teil? - Wie viele LPs mehr nahmen am
Action Bound Angebot im Vergleich
zur Schach AG teil? - Kreuze die richtigen Kästchen an.
Aussage
ja
nein
nicht
eindeutig
An der Leichtathletik AG nehmen die
meisten LPs teil.
In der Brettspiel und Kartenspiel AG sind mehr LPs als bei der Action Bound AG.
In der Fußball AG sind mehr LPs als bei
fünf AGs mit den wenigsten.
In der Häkel AG sind mehr LPs als in
der Märchen AG.
Wenn mehr LPs Schach spielen könnten, wären auch mehr LPs in der Schach AG.
4
Das Säulendiagramm zeigt dir die Jahresnoten der Klassen 9 a und 9 b.
Schaue dir zuerst das Diagramm genau an und löse dann die Aufgaben.
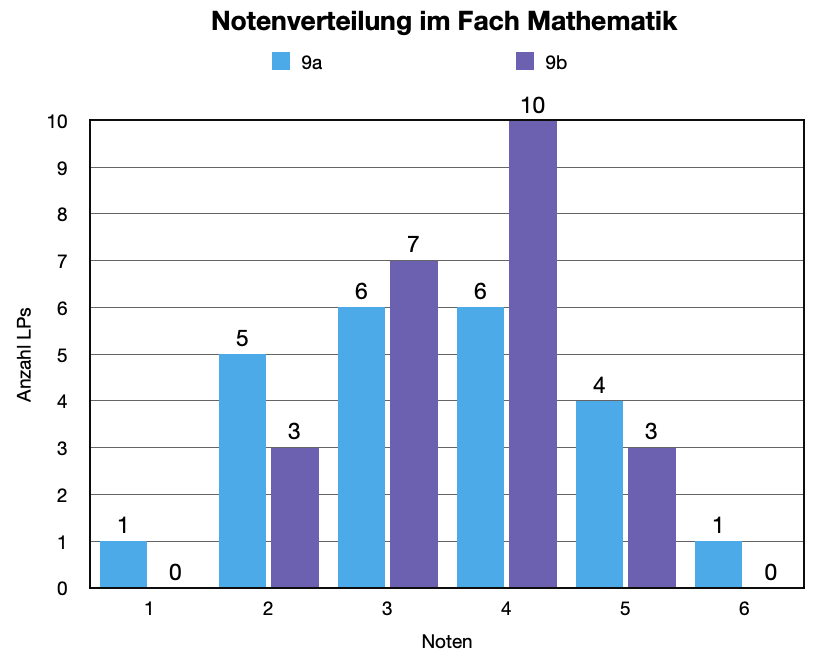
Schaue dir zuerst das Diagramm genau an und löse dann die Aufgaben.
- Wie viele LPs sind in der jeweiligen Klasse?
- Bei welcher Note ist die Abweichung
zwischen den beiden Klassen am größten? - Welchen Durchschnitt, auf Zehntel
gerundet, haben die jeweiligen Klassen
erreicht? - Überlege dir drei Aussagen zu dem
Diagramm.
Hinweis: Dass die eine Säule hellblau
und die andere dunkelblau ist, wäre
keine Aussage.
1 % entspricht 3,6°
5
Das Säulendiagramm zeigt dir die durchschnittlichen
Entfernungen an, die die LPs zur Schule zurücklegen
müssen.
Schaue dir zuerst das Diagramm genau an und
löse dann die Aufgaben.
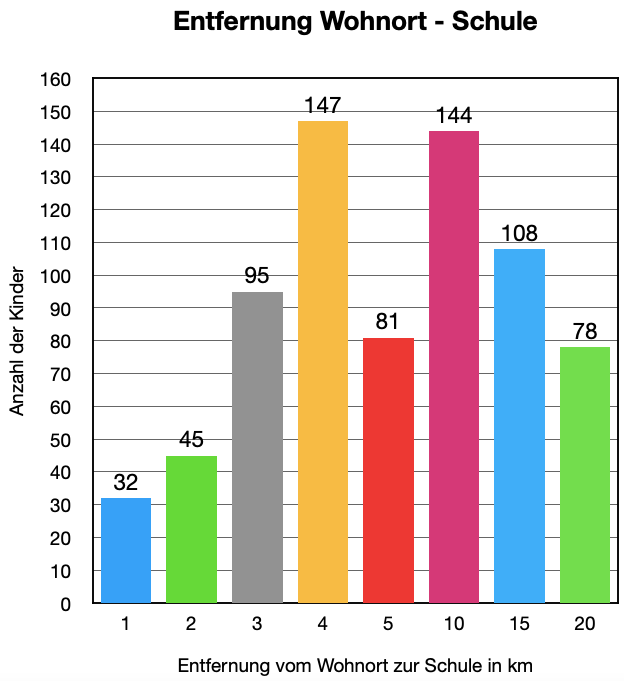
Entfernungen an, die die LPs zur Schule zurücklegen
müssen.
Schaue dir zuerst das Diagramm genau an und
löse dann die Aufgaben.
- Wie viele LPs sind an der Schule?
- Welche zwei Entfernungen wurden am
häufigsten genannt? - Wie viele Kilometer legt jeder LP im Durchschnitt
zurück?
Runde dein Ergebnis auf Hundertstel. - Berechne die relative Häufigkeit der einzelnen
Kilometerentfernungen und stelle diese in
einem Kreisdiagramm dar.
Erstelle dafür zuerst eine Tabelle.
6
In diesem Diagramm siehst du die Gewinne und Verluste der Kiosk AG an einer Schule.
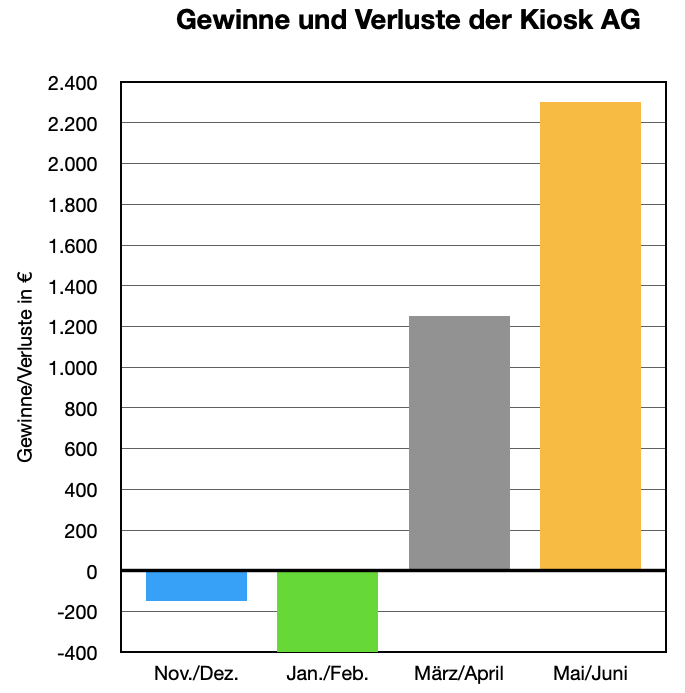
- Wie hoch ist der Reingewinn in den acht Monaten?
Lese die einzelnen Werte möglichst genau aus
dem Diagramm ab (auf 10er). - Um den Verlust aus den Monaten November
bis Februar zu verringern, werden im nächsten
Jahr zusätzlich Waffeln verkauft. Damit wird der
Verlust im Nov./Dez. des folgenden Jahres um
2/3 verringert. Im Jan./Feb. kann der Verlust sogar
um 90 % verringert werden.
Wie hoch sind die Verluste dann noch in den
ersten vier Monaten?
Rechenweg
Um die volle Punktzahl zu erhalten, solltest du für das Lösen der Aufgaben stets den Rechenweg angeben.
Buche
7
Hier siehst du die Bilder einer Fichte und einer Buche.
Beide Baumarten wachsen unterschiedlich schnell.
Die Fichte wächst recht gleichmäßig 50 cm im Jahr.
Die Buche wächst die ersten zehn Jahre nur 30 cm pro Jahr
und dann jährlich 55 cm.
Beide Baumarten wachsen unterschiedlich schnell.
Die Fichte wächst recht gleichmäßig 50 cm im Jahr.
Die Buche wächst die ersten zehn Jahre nur 30 cm pro Jahr
und dann jährlich 55 cm.
Fichte
- Fülle die Wertetabelle für die ersten 30 Jahre aus.
- Nach wie vielen Jahren hat die Buche die Fichte eingeholt?
- Angenommen die Buche ist bei ihrer Pflanzung bereits 2 m groß.
Kann die Fichte die Buche dann noch einholen?
Jahr
1
3
5
10
11
15
20
30
Höhe Fichte
in m
0,5 m
5,5 m
Höhe Buche
in m
3,55 m
