TitelDer Umfang (Definition)
AutorMNWeG
veröffentlicht14.01.2022
FachMathematik
KompetenzbereichMessen
NiveaustufeM (Mindeststandard)
Phase5
MaterialformInformation

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Was ist der Umfang einer Fläche?

Läuft man (gedanklich) ein Mal um die Fläche herum - genau auf den Seiten - dann ist man den Umfang der Fläche abgelaufen. Zählt man nun alle Schritte zusammen, hat man den Umfang.

Definition Umfang

1. Der Umfang einer Fläche ist die Summe aller Seiten.

2. In der Mathematik kürzt man den Umfang mit einem großen $U$ ab.

Um kenntlich zu machen, was für einen Umfang man berechnet, setzt man hinter das $U$ noch eine kleine Bezeichnung. Da Jonas den Umfang eines Rechtecks berechnet, bietet sich hierfür also ein kleines Rechteck an: $U_{□}$

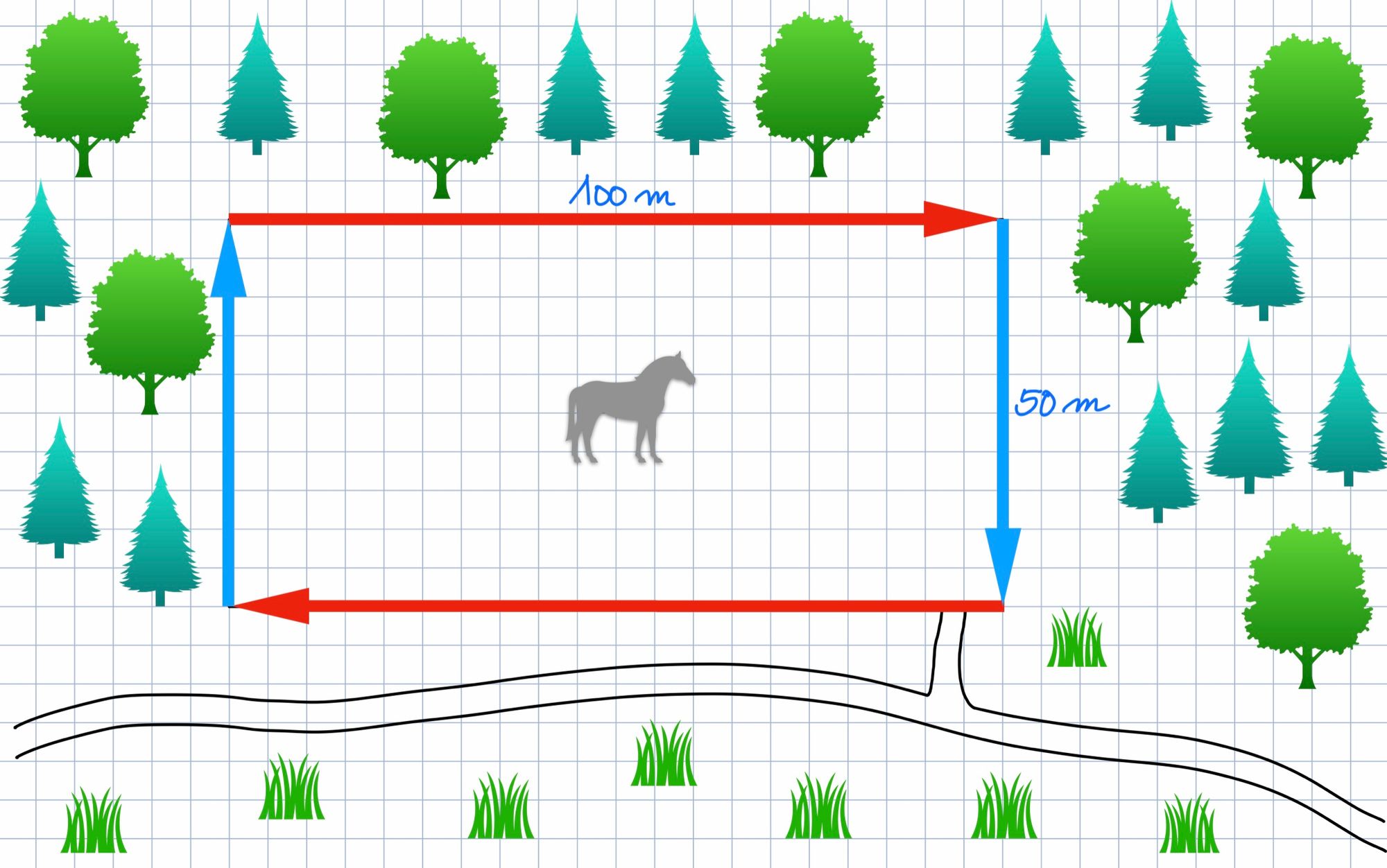
Wie wird der Umfang eines Rechtecks berechnet?

Die Pferdekoppel von Jonas hat vier Seiten:

Seite $a = 100 m$ (diese Seite gibt es zwei Mal),

Seite $b = 50 m$ (diese Seite gibt es auch zwei Mal).

Den Umfang der Pferdekoppel ( $U_{□}$ ) berechnet Jonas also wie folgt:

$U_{□} = a + b + a + b = 100 m + 50 m + 100 m + 50 m = \underline{\underline{300m}}$

Wichtige Begriffe: Maßzahl

Um zu beschreiben, wie groß, schwer, breit, lang, tief, hoch, ... etwas ist oder wie lange etwas dauert, nutzen wir Maßzahlen.

Soll zum Beispiel beschrieben werden, wie viele Minuten eine Stunde dauert, dann sagt man: 60 Minuten.

Soll die Höhe eines Turmes angegeben werden, dann sagt man: 300 Meter.

Soll das Gewicht des Eiffelturms beschrieben werden, sagt man: 7.341.214 Kilogramm.

Merke:

Die Maßzahl ist das Ergebnis einer Messung und steht vor der Maßeinheit.

Wichtige Begriffe: (Maß-) Einheit(en)

Wenn man mit Maßzahlen hantiert, muss man aber auch die (Maß-) Einheit dazuschreiben:

Wenn angegeben wird, wie viel etwas kostet, dann gibt man die Geldeinheit an.

Z.B.: $€$ für Euro oder $c t$ für Cent.

Wenn angegeben wird, wie viel etwas wiegt, dann gibt man die Gewichtseinheit an.

Z.B.: $t$ für Tonnen, $k g$ für Kilogramm, $g$ für Gramm und $m g$ für Milligramm.

Wenn angegeben wird, wie lange etwas dauert, gibt man die Zeiteinheit an.

Z.B.: $d$ für Tage, $h$ für Stunden, $min$ für Minuten und $se k$ für Sekunden.

Und da beim Umfang $U$ eine Länge angegeben wird, nutzt man hierfür natürlich die Längeneinheiten!

Merke:

Der Umfang ( $U$ ) wird in Längeneinheiten angegeben. Dies können sein:

1. $km$ für Kilometer (Kilo bedeutet $1000$ → $1 km$ sind also $1000 M e t er$ )

2. $m$ für Meter

3. $d m$ für Dezimeter (Dezi bedeutet $10 t e l$ → $1 m$ sind also $10 Dez im e t er$ )

4. $c m$ für Zentimeter (Zenti bedeutet $100 t e l$ → $1 m$ sind also $100 Z e n t im e t er$ )

5. $mm$ für Millimeter (Milli bedeutet $1000 t e l$ → $1 m$ sind also $1000 M i ll im e t er$ )

Beispiel:

24 ist die Maßzahl

m ist die (Maß)Einheit

U_{□} = 24 m