Name: Materialnetzwerk e. G.
Address: Endersstr. 33, Wutöschingen, BW, 79793
Telephone: +49 7746 92 85 70

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Über Jahre hinweg hat Jonas' Opa die Wiese nicht mehr gemäht und es hat sich teilweise ein richtiges Dornengestrüpp gebildet.

Jonas: Puh! Das wird ganz schön viel Arbeit! Am besten fange ich gleich mal an!
Vater: Langsam, Jonas! Es ist schon 19 Uhr. Das schaffst du heute nicht mehr! Für diese Fläche brauchst du sicher ganz schön lange!

Jonas: Fläche? Was bedeutet das?
Vater: Nun... im Gegensatz zu einer Länge hat eine Fläche zwei Dimensionen: eine Länge und eine Breite. Wenn man diese beiden Größen miteinander multipliziert, erhält man den Flächeninhalt.
Jonas: Waaaas? Ich kapier gar nichts!
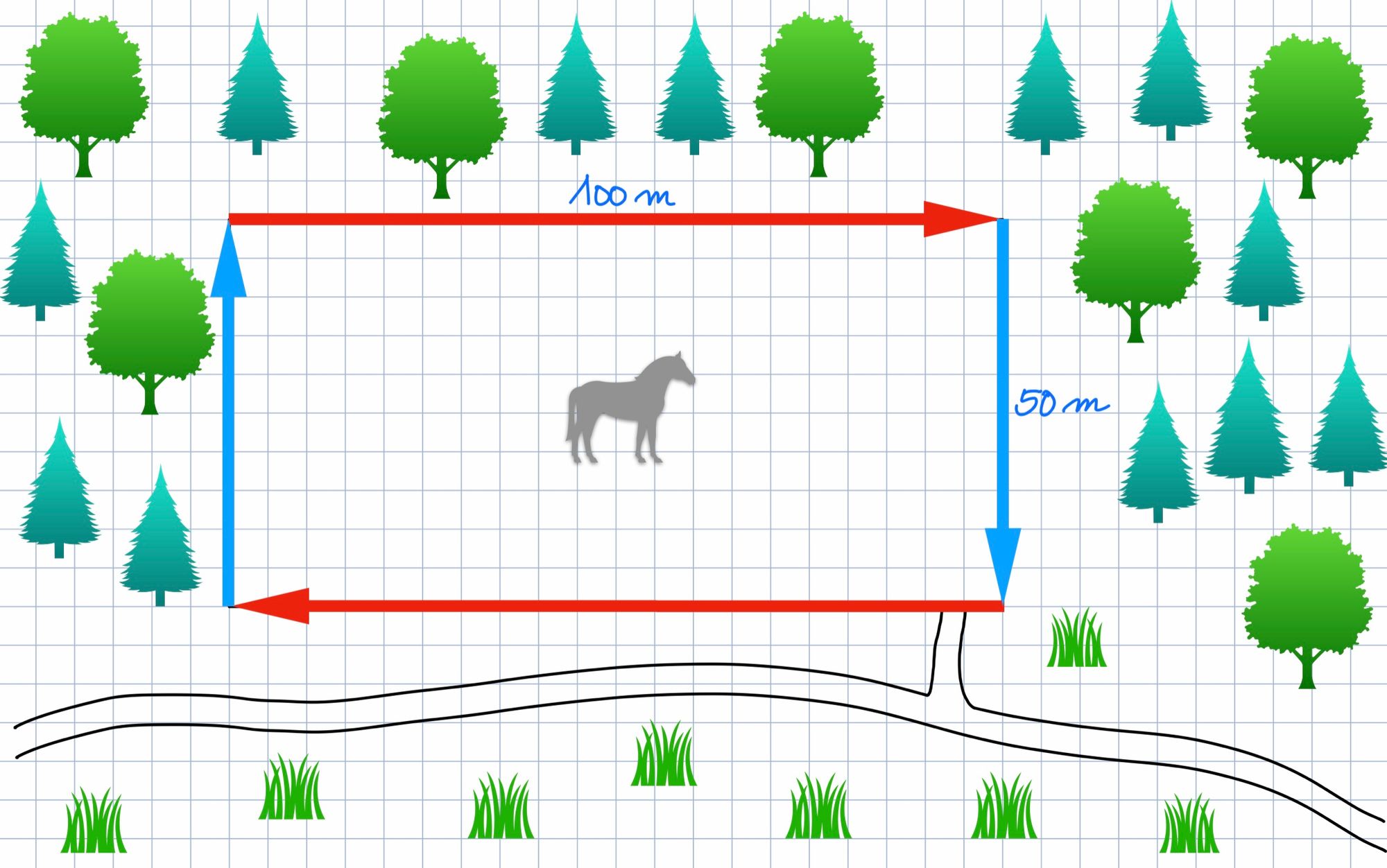
Vater: Also: Stell dir vor, du unterteilst die Pferdekoppel in Quadrate. Und die Quadrate sind $10 m$ lang und $10 m$ breit. Wie viele Quadrate passen dann in die Pferdekoppel?
Regieanweisung: Jonas kratzt sich am Kopf und überlegt.

Bevor du weiterliest:

Kannst du Jonas helfen?

Was glaubst du: Wie viele Quadrate mit $10 m$ Länge und $10 m$ Breite passen auf die Pferdekoppel, die $100 m$ lang und $50 m$ breit ist?

(Die Lösung findest du auf der nächsten Seite.)

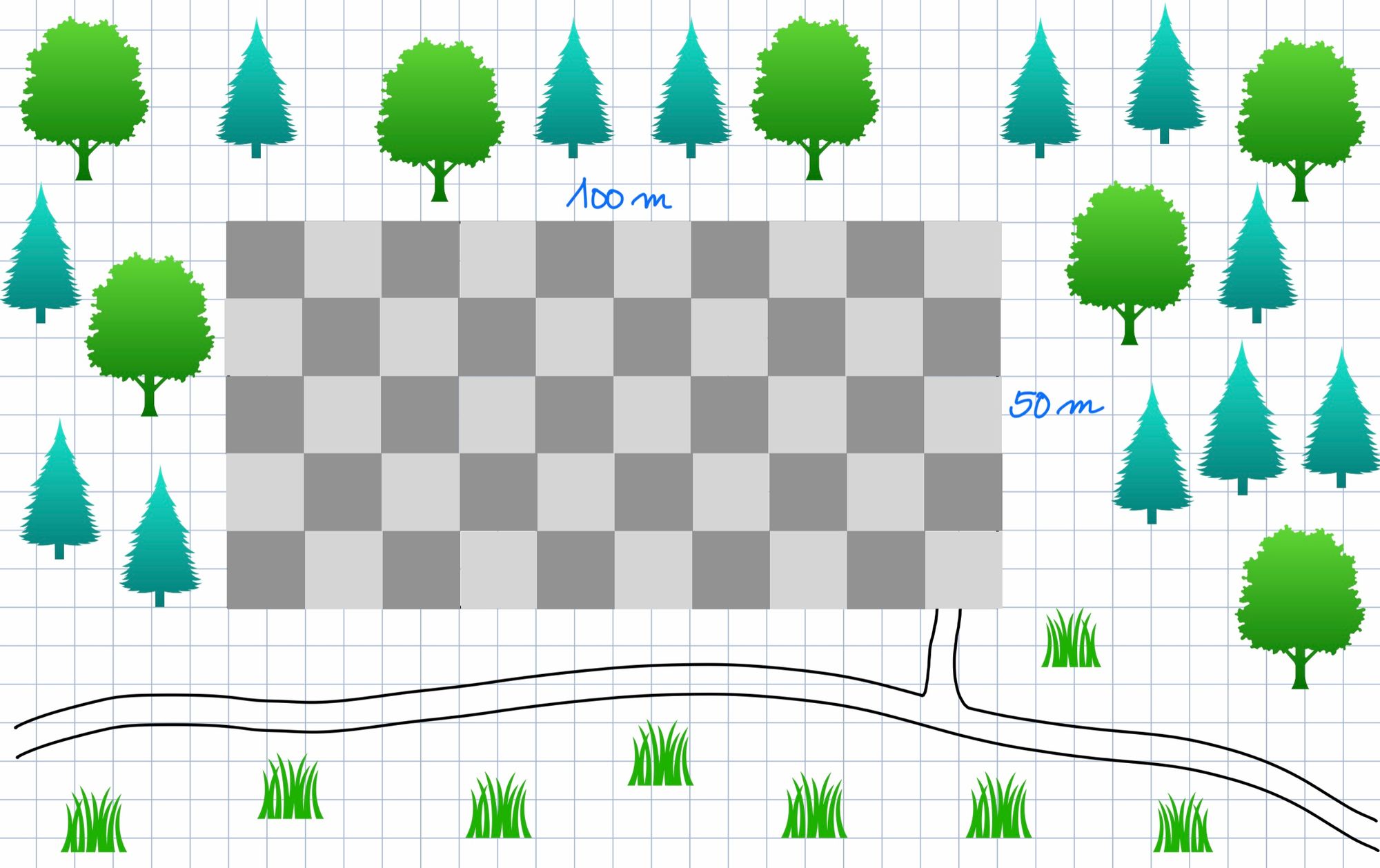
Jonas: Also: Wenn die Koppel $100 m$ lang ist, dann passen in der Länge zehn solche Quadrate hinein.
Denn $10 \cdot 10 m = 100 m$ .
Und weil die Koppel $50 m$ breit ist, passen fünf solche Quadrat-Reihen hinein.
Denn $5 \cdot 10 m = 50 m$ .
Wenn also fünf Reihen mit jeweils zehn Quadraten hineinpassen, sind es insgesamt $50$ Quadrate!
Vater: Ganz genau! Und wenn du für ein Quadrat.... hmmm.... also ich schätze mal $10$ Minuten zum Mähen brauchst, wie lange brauchst du dann für die ganze Koppel?
Jonas: Das ist einfach!
Wenn ich für ein Quadrat $10$ Minuten brauche, dann brauche ich für $50$ Quadrate $50$ Mal so lange, also $500$ Minuten!
Und das sind $8$ Stunden und $20$ Minuten!
Vater: Richtig! Da siehst du: Für die gesamte Fläche brauchst du ganz schön lange. Da wirst du heute nicht mehr fertig!
Jonas: Na gut. Dann mache ich das am Samstag!