Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
1
Kreuze die richtigen Aussagen an.
2
In einem Dreieck sind die Winkel β = 25° und γ = 65° gegeben.
- Berechne den Winkel α.
- Um welche Art von Dreiecken handelt es sich?
3
Stelle dir ein gleichseitiges Dreieck vor. Eventuell hilft es dir eine kleine Skizze anzufertigen.
- Wie groß sind die einzelnen Winkel?
- Wie lang sind die Seiten?
4
In einem rechtwinkligen Dreieck beträgt der Winkel α = 40°.
- Wie groß sind die einzelnen Winkel?
- Wie viele Lösungen gibt es?
5
In einem gleichschenkligen Dreieck beträgt der Winkel β = 42°.
- Berechne die fehlenden Winkel.
- Wie viele Lösungen gibt es?
- Um welche Dreiecksarten handelt es sich noch?
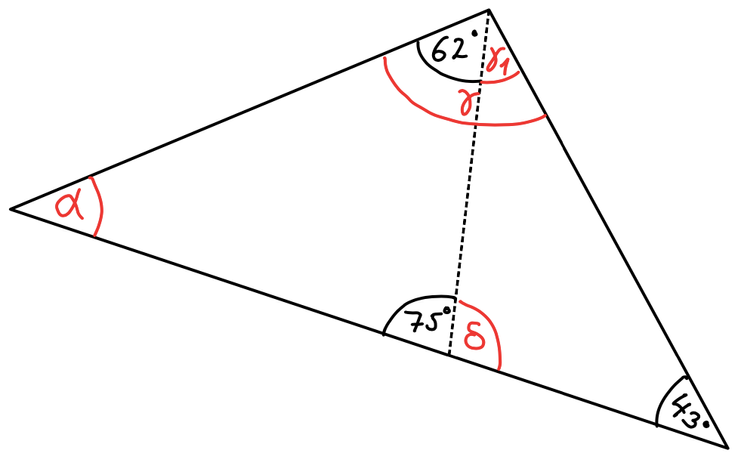
6
- Berechne die fehlenden Winkel. Achtung: Messen führt zu falschen Ergebnissen!
- Um welche Art von Dreieck handelt es sich?
