Was ist Kürzen und Erweitern?
Es kommt oft vor, dass 2 verschiedene Brüche den selben Anteil beschreiben. Folgendes Beispiel verdeutlicht das:
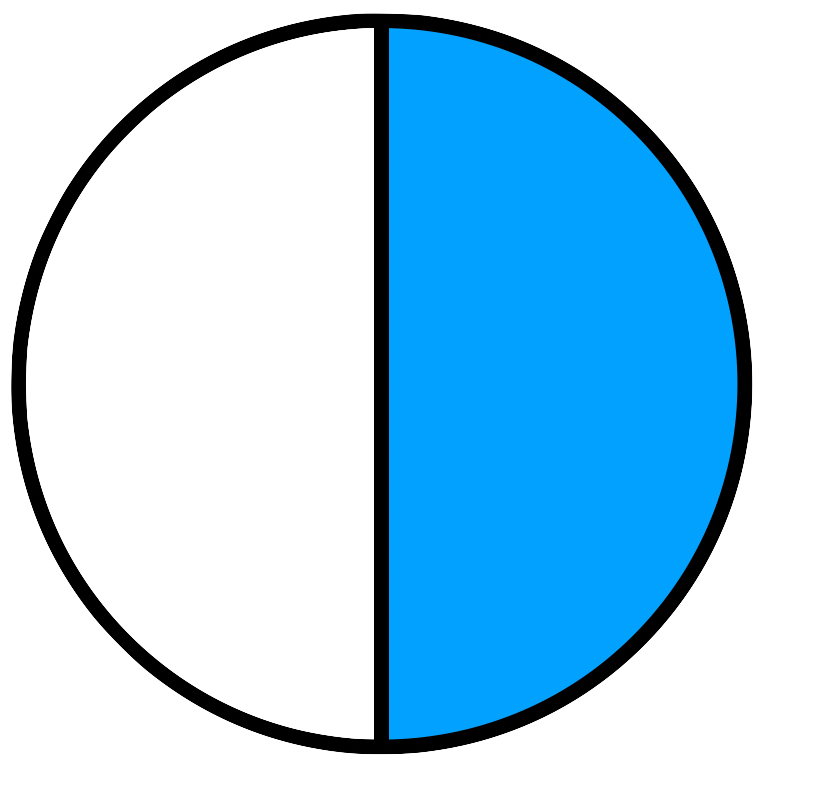


Teilt man beispielsweise einen Kuchen in 2 Teile und isst 1 davon (linke Grafik), so hat man insgesamt 21 des Kuchens gegessen. Hätte man den Kuchen in 4 Teile unterteilt und 2 Teile davon gegessen, so hätte man 42 des Kuchens gegessen (rechte Grafik). Wie man an den zwei Grafiken erkennen kann, sind die zwei blau eingefärbten Flächen, also 21 und 42 gleich groß.
Erweitern = Verfeinern
Denken wir zurück an die Balkentafel: Einen Balken kann man verfeinern, indem man ihn mit einer ganzen Zahl multipliziert. Beispielsweise einen 2er-Balken kann man mit 2 multiplizieren und man erhält einen 4er-Balken.
Wie wir anhand der Grafik sehen können, ist dann der Anteil an einem Ganzen (die blau eingefärbte Fläche) immer noch gleich groß.

Wie man auf der formalen Ebene erweitert bzw. verfeinert, siehst du im nächsten Infokasten.
https://editor.mnweg.org/mnw/dokument/erweitern-von-bruechen-8
Das Erweitern von Brüchen kann man auch als ein Verfeinern sehen. Denken wir zurück an die Balkentafel oder das Kuchen-Beispiel, so erweitern wir, indem wir die blau eingefärbte Fläche noch feiner unterteilen.
Einen Bruch erweitert man, indem man sowohl Zähler, als auch Nenner mit der selben Zahl multipliziert.
Um von 21 zu 42 zu gelangen, muss man den Zähler (die 1) und den Nenner (die 2) mit 2 multiplizieren.


Beispiele

1.
Aus 43 werden 129 , indem man Zähler (3) und Nenner (4) jeweils mit 3 multipliziert.

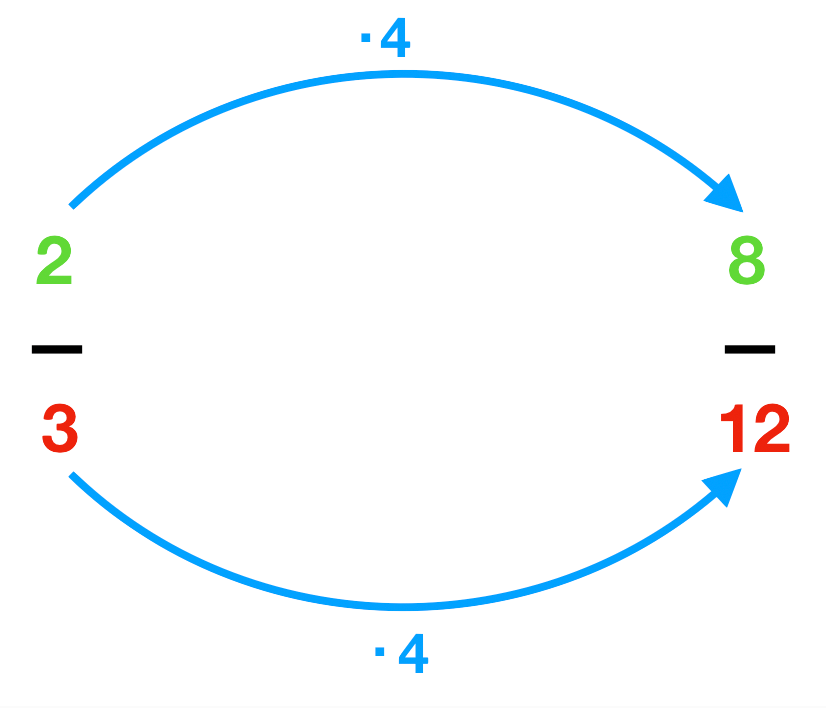
2.
Aus 32 werden 128 , indem man Zähler (2) und Nenner (3) jeweils mit 4 multipliziert.

https://editor.mnweg.org/mnw/dokument/erweitern-von-bruechen-8


