Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
1
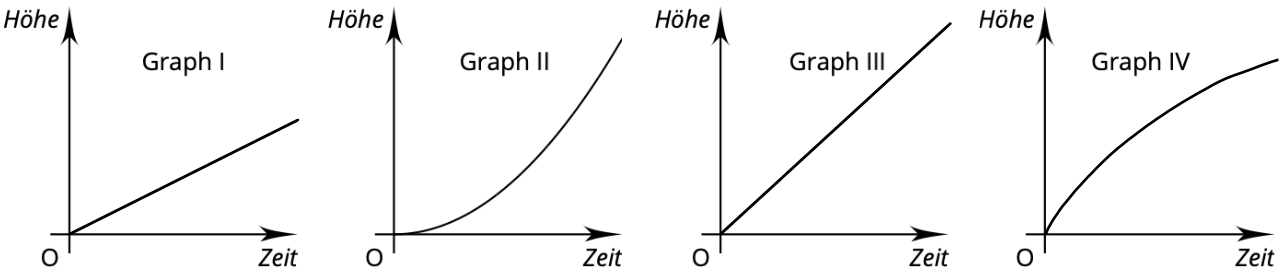
Hier siehst du vier Gefäße, die gleichmäßig mit Wasser befüllt werden.
Welches Gefäß gehört zu welchem Graphen? Schreibe die Lösungspaare auf.
Welches Gefäß gehört zu welchem Graphen? Schreibe die Lösungspaare auf.
Angebot 2
bis 100 Einheiten: 3,5 Cent
ab 101 Einheiten: 1,8 Cent
Angebot 1
Grundgebühr: 1,99 €
Preis pro Einheit: 1,5 Cent
2
Du hast drei verschiedene Telefontarifangebote.
- Welches Angebot gehört zu welchem Graphen?
- Welcher Tarif ist am günstigsten, wenn Paul
150 Einheiten im Monat vertelefoniert?
Angebot 3
Preis pro Einheit: 2,9 Cent
3
Ergänze in der Wertetabelle die fehlenden Werte. Die Funktionsgleichung lautet: f(x) = 2x - 1
x
-2
-1
0
1
2
3
f(x) = y
- 5
3
4
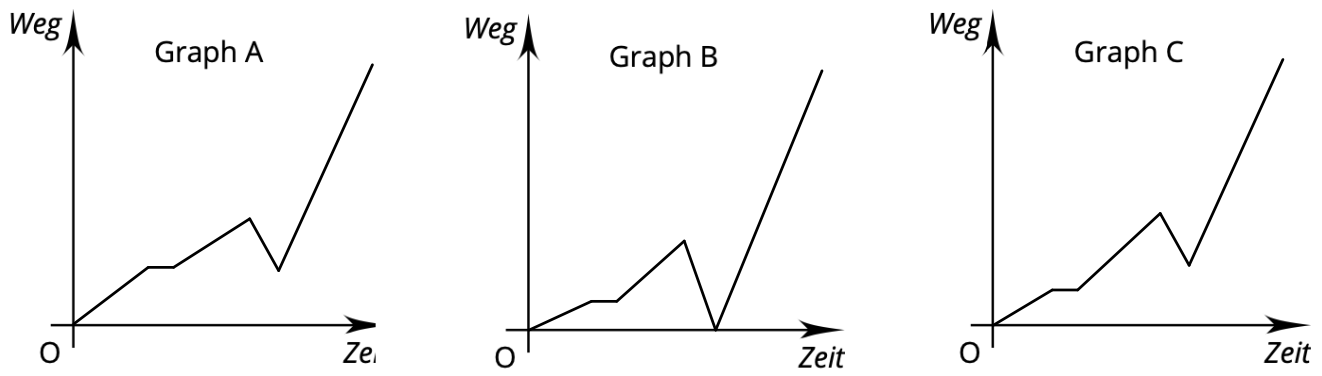
Fritz läuft von zu Hause langsam Richtung Schule los. Nach kurzer Zeit bleibt er stehen, da die Ampel rot ist. Er läuft nun etwas schneller weiter, um kurz darauf festzustellen, dass er seine Mütze verloren hat. Schnell rennt er ein Stück des Weges zurück, um dann mit der Mütze auf dem Kopf im Sprint zur Schule zu rennen.
Welcher Graph passt zu der Geschichte?
Welcher Graph passt zu der Geschichte?
5
Welche Funktionsgleichung gehört zu welchem Graphen?
Schreibe den jeweiligen Buchstaben in das Kästchen davor.
Schreibe den jeweiligen Buchstaben in das Kästchen davor.
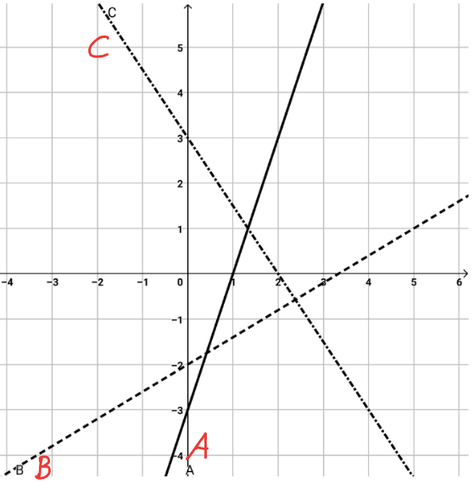
f(x) = x - 2
f(x) = - 1,5 x + 3
f(x) = 3x - 3
6
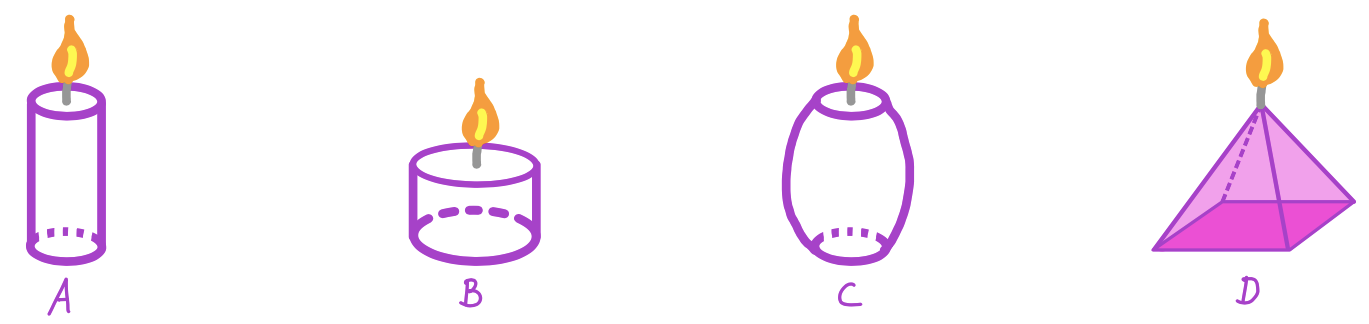
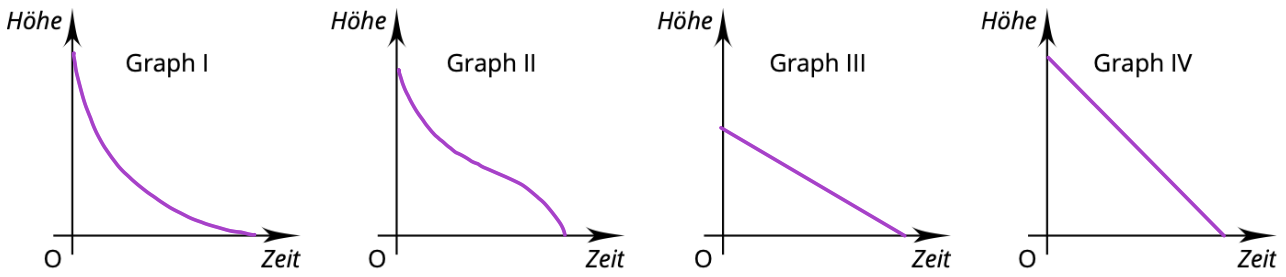
Hier siehst du vier Kerzen, die gleichmäßig abbrennen.
Welche Kerze gehört zu welchem Graphen? Schreibe die Lösungspaare auf.
Welche Kerze gehört zu welchem Graphen? Schreibe die Lösungspaare auf.
7
Zwei Freunde machen eine Fahrt mit dem ICE. Leider sitzen sie nicht im gleichen Zug.
Fritz fährt von Hamburg nach München und Klaus von Freiburg nach Berlin.
In dem Diagramm siehst du stark vereinfacht die Graphen zu ihren Reisen und ihre
Entfernung in Luftlinie.
Fritz fährt von Hamburg nach München und Klaus von Freiburg nach Berlin.
In dem Diagramm siehst du stark vereinfacht die Graphen zu ihren Reisen und ihre
Entfernung in Luftlinie.
- Wie weit sind die beiden zu Beginn ihrer Reise voneinander entfernt?
- Um wie viel Uhr kreuzen sich die beiden Freunde?
- Wie viele Kilometer haben die beiden Freunde bis zu ihrem Kreuzungspunkt
jeweils zurückgelegt?
Intercity, Doppelstock
8
Auf welche Diagramme treffen folgende Aussagen zu?
- Die Züge fahren gleich schnell.
- Die Züge fahren zur gleichen Uhrzeit los.
- Beide Züge bewegen sich.
- Ein Zug ist schneller als der andere.
Stehende Züge im Bahnhof
Diagramm 1
Diagramm 2
Diagramm 3
Privat: A. Schöler
9
Hier siehst du die Höhenmeter, die eine Wandergruppe im Laufe eines Tages zurückgelegt hat.
- Wie viele Stunden war die Wandergruppe unterwegs?
- Wie viele Höhenmeter (alles nach oben) hat sie dabei bewältigt?
- Wann ging es weder bergauf noch bergab?
- Nachgedacht: Kannst du sagen, wann die Gruppe eine Pause gemacht haben könnte?
Begründe deine Aussage.
Berggipfel
10
In einer Küche sollen neue Fliesen verlegt werden. Es gibt zwei Angebote für Fliesen im
Baumarkt. Die Küche hat eine Größe von 16 m2.
Baumarkt. Die Küche hat eine Größe von 16 m2.
- Wie viele Fliesen pro Angebot würde man für die ganze Küche benötigen?
- Wie viel Euro kann man sparen, wenn man die günstigeren Fliesen nimmt?
- Wie viel Prozent mehr kosten die teureren Fliesen?
- Wie hoch sind die Gesamtkosten bei Angebot A, wenn noch Nebenkosten von
23 % entstehen? - Nachgedacht: Warum wird es eventuell schwierig, wenn man genau die passende Menge Fliesen kauft? Begründe deine Meinung.
Angebot A
Angebot B
20 cm x 30 cm
3,90 € / Stück
65 € / m2
20 cm x 40 cm
4,80 € / Stück
60 € / m2
