Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Nachdem du nun weißt, wie man unechte Brüche in gemischte Zahlen umwandelt, lernst du hier, wie man es auch andersherum macht - also wie man aus gemischten Zahlen unechte Brüche macht.

Wieder muss man eigentlich nur zwei Fragen stellen:

1. Was ist das Produkt aus Nenner und ganzer Zahl?

2. Was ist die Summe aus dem Ergebnis des 1. Schrittes und dem Zähler?

Hier siehst du die Vorgehensweise am Beispiel der gemischten Zahl $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 3\frac{4}{5}$ :

Was ist das Produkt aus Zähler und ganzer Zahl?

Antwort:

\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 15

mal. Denn:

\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 5\cdot 3 = 15

Was ist die Summe aus 15 und dem Zähler?

Antwort:

\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 18

. Denn:

\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 15+4=19

Wie lautet also der unechte Bruch?

Antwort:

\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{19}{5}

Schritt 3:

Ergebnis aus Schritt 1 und 2 als neuen Zähler aufschreiben.

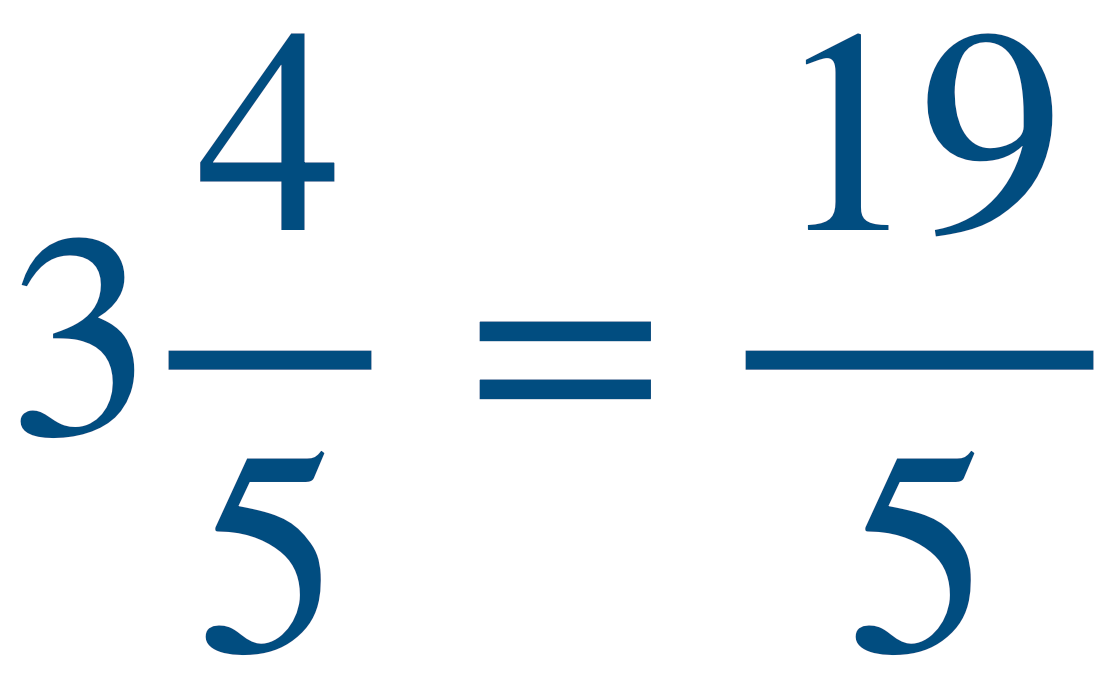
Schritt 2:

Ergebnis aus Schritt 1 mit dem Zähler addieren

( $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 15+4=19$ ).

Schritt 1:

Nenner und ganze Zahl multiplizieren

( $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 5⋅3=15$ ).

Schritt 4:

Nenner übernehmen.

Warum ist das so?

Sehen wir uns nochmals die gemischte Zahl $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 3\frac{4}{5}$ an.

Sie hat zwei Bestandteile: die ganze Zahl $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 3$ und den Bruch $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{4}{5}$

Die ganze Zahl $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 3$ kann auch als Bruch mit dem Nenner $\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 5$ geschrieben werden.

Denn es gilt:

$\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 3=1+1+1=\frac{5}{5}+\frac{5}{5}+\frac{5}{5}=\frac{15}{5}$

Da wir die gemischte Zahl ja in einen unechten Bruch umformen wollen, bleibt der Bruch einfach bestehen.

\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{4}{5}

Nun führen wir die beiden Bestandteile wieder zusammen und addieren also die zwei Brüche:

Als Ergebnis erhalten wir so einen unechten Bruch mit dem gleichen Wert der gemischten Zahl!

\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{15}{5}+ \frac{4}{5}= \bold{\frac{19}{5}}

Gemischte Zahlen umwandeln

Was ist eine gemischte Zahl? Wie verwende ich eine gemischte Zahl? Wie wandle ich eine gemischte Zahl um?

YouTube-Video

Link: https://youtu.be/XdldM_TvFk8