HerunterladenAls PDF Herunterladen
  • Gleichungen R 8 |B|
  • MNWeG
  • 22.12.2022
  • Mathematik
  • Gleichungen
  • R (Regelstandard)
  • 8
  • Gelingensnachweis
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
GN
Gleichungen R 8 |B|
Mathematik Gleichungen R 8

Löse alle Auf­ga­ben auf einem ka­rier­ten Block-​Blatt.

Fol­gen­de Ma­te­ri­a­li­en sind er­laubt: Stif­te. (kein Ta­schen­rech­ner!)

Dauer: ca. 60 Mi­nu­ten.

1
Wenn ja, um wel­che bi­no­mi­sche For­mel han­delt es sich? Kreu­ze an.
3 / 3
1. binom. For­mel
2. binom. For­mel
3. binom. For­mel
keine binom. For­mel
2x² - 4x + 4
(3u - 7z)(3u + 7z)
3x² - 6x² - 9x²
25x² - 64y²
36 + 12x + x²
20x³ - 4x + 5
2
Vereinfache die Terme mit Hilfe einer binomischen Formel.
6 / 6
  • (1x-8)² =
  • (2y-8z)(2y+8z) =
  • (4y-5z)(4y+5z) =
  • (2+9x)² =
  • (9+5x)² =
  • (8y-6z)² =
3
Oh, hier haben sich bei der bi­no­mi­schen For­mel Feh­ler ein­ge­schli­chen. (2 P)
Be­schrei­be diese und schrei­be die For­mel rich­tig auf. (1 P)
3 / 3
  • (a + 6)² = a² - 36

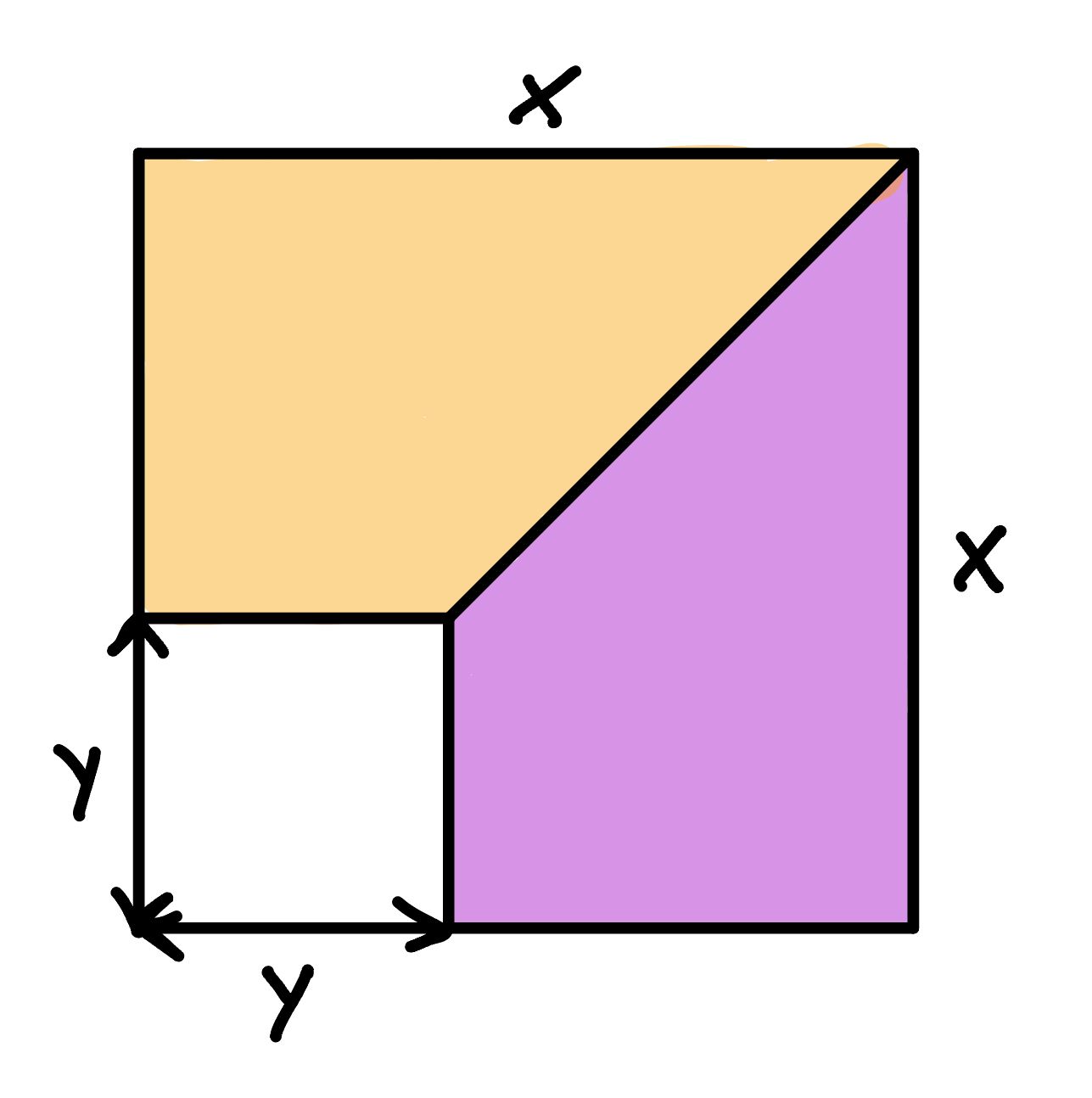
4
Er­mitt­le den Flä­chen­in­halt des Qua­drats rech­ne­risch
 mit einer bi­no­mi­schen For­mel. (2 P.)
Um wel­che bi­no­mi­sche For­mel
han­delt es sich? Nenne diese. (1 P.)
3 / 3
Bereitgestellt von: MNWeG Stand: 20.02.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/gleichungen-r-8-b
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/gleichungen-r-8-b
GN
Gleichungen R 8 |B|
Mathematik Gleichungen R 8
5
Be­rech­ne den Schnitt­punkt S mit dem ge­eig­ne­ten Ver­fah­ren.
8 / 8
  • I.10y = 32 - 4x
    II. y = 29 - 9x

  • I. y = -15 + 6x
    II. y = -19 + 7x

  • I. 7y = 33 - 1x
    II. y = 34 - 6x

  • I. 10x + 6y = 26
    II. 5x - 6y = 4

6
Frau Weiß kauft sechs Bröt­chen und vier Bre­zeln. Sie be­zahlt 6,80 €. Am an­de­ren Tag kauft ihr Sohn vier Bröt­chen und vier Bre­zeln. Er be­zahlt 5,20 €.
2 / 2
  • Stel­le ein li­ne­a­res Glei­chungs­sys­tem auf. (1 P)
  • Er­klä­re wofür die Va­ri­a­ble x und y ste­hen. (1 P)
7
Oh nein, die Was­ser­fle­cken haben die Zah­len ver­wischt. Kor­ri­gie­re die Kleck­se und löse das li­ne­a­re Glei­chungs­sys­tem.
2 / 2
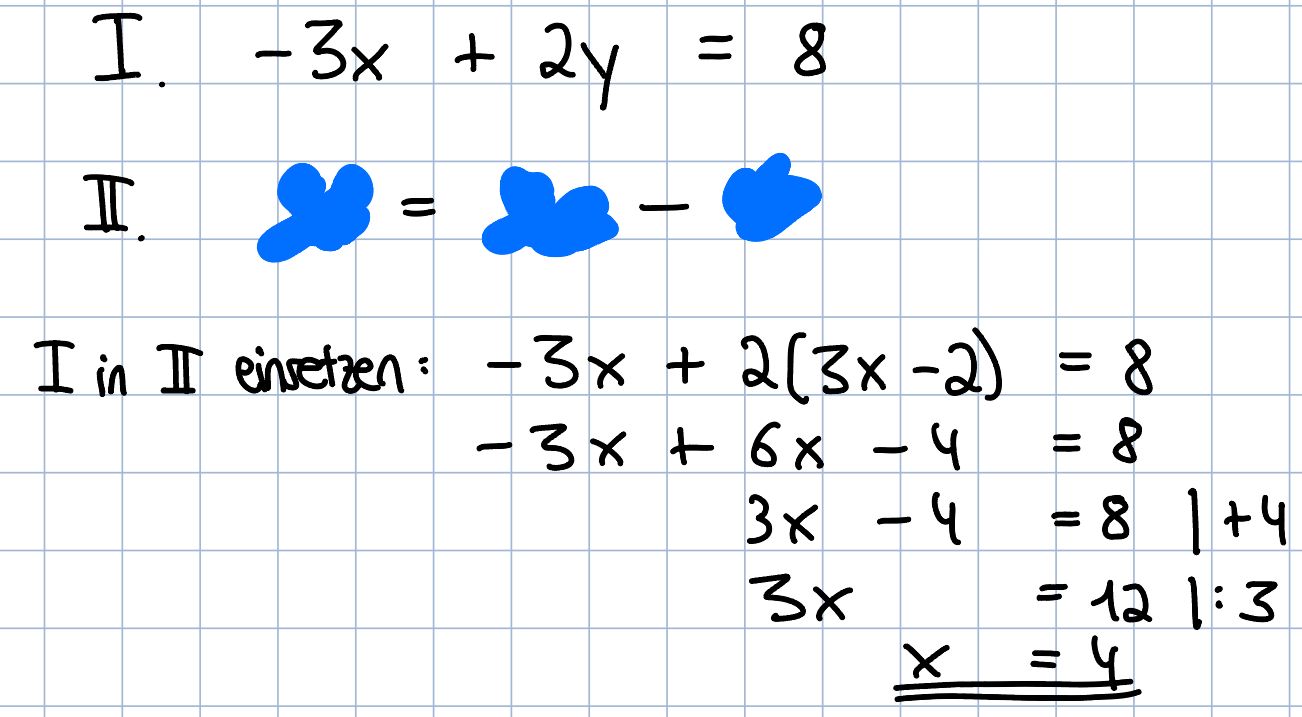
8
Ein Hotel ver­fügt über 105 Bet­ten sowie 40 Zim­mer. Es gibt Zwei- und Drei­bett­zim­mer. Wie viele Zwei-​und-Dreibettzimmer hat das Hotel?

Stel­le ein li­ne­a­res Glei­chungs­sys­tem auf. Er­mitt­le durch Lösen des li­ne­a­ren Glei­chungs­sys­tems die An­zahl der Drei­bett­zim­mer und der Dop­pel­zim­mer und schrei­be einen Ant­wort­satz.
3 / 3
Du hast von 30 Punkten erreicht (bestanden bei 25 Punkten).
Bereitgestellt von: MNWeG Stand: 20.02.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/gleichungen-r-8-b
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/gleichungen-r-8-b
x