Name: Materialnetzwerk e. G.
Address: Endersstr. 33, Wutöschingen, BW, 79793
Telephone: +49 7746 92 85 70

TitelGrundrisse zeichnen und berechnen
AutorMNWeG
veröffentlicht14.01.2022
FachMathematik
KompetenzbereichMessen
NiveaustufeR (Regelstandard)
Phase5
MaterialformArbeitsblatt

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Zeichne auf einem karierten Blatt Papier beliebige Grundrisse von Zimmern und berechne ihren Umfang und Flächeninhalt!
Es können verrückte und verschachtelte, aber auch echte Zimmer sein!

Achte darauf, dass du nur entlang der Kästchen zeichnest (also nicht schräg oder diagonal).
Achte darauf, dass die Seiten immer ganzzahlige Längen haben (also 3, 4, 5, ... cm).
Berechne den Umfang und den Flächeninhalt des Zimmers.
Achte auf eine korrekte Schreibweise (4-Schritt-Löseverfahren).
Lass deine Rechnungen von einem Profi überprüfen! 😉

Beispiel:

1. Zeichne ein verrücktes Zimmer.

2. Teile es in Flächen.

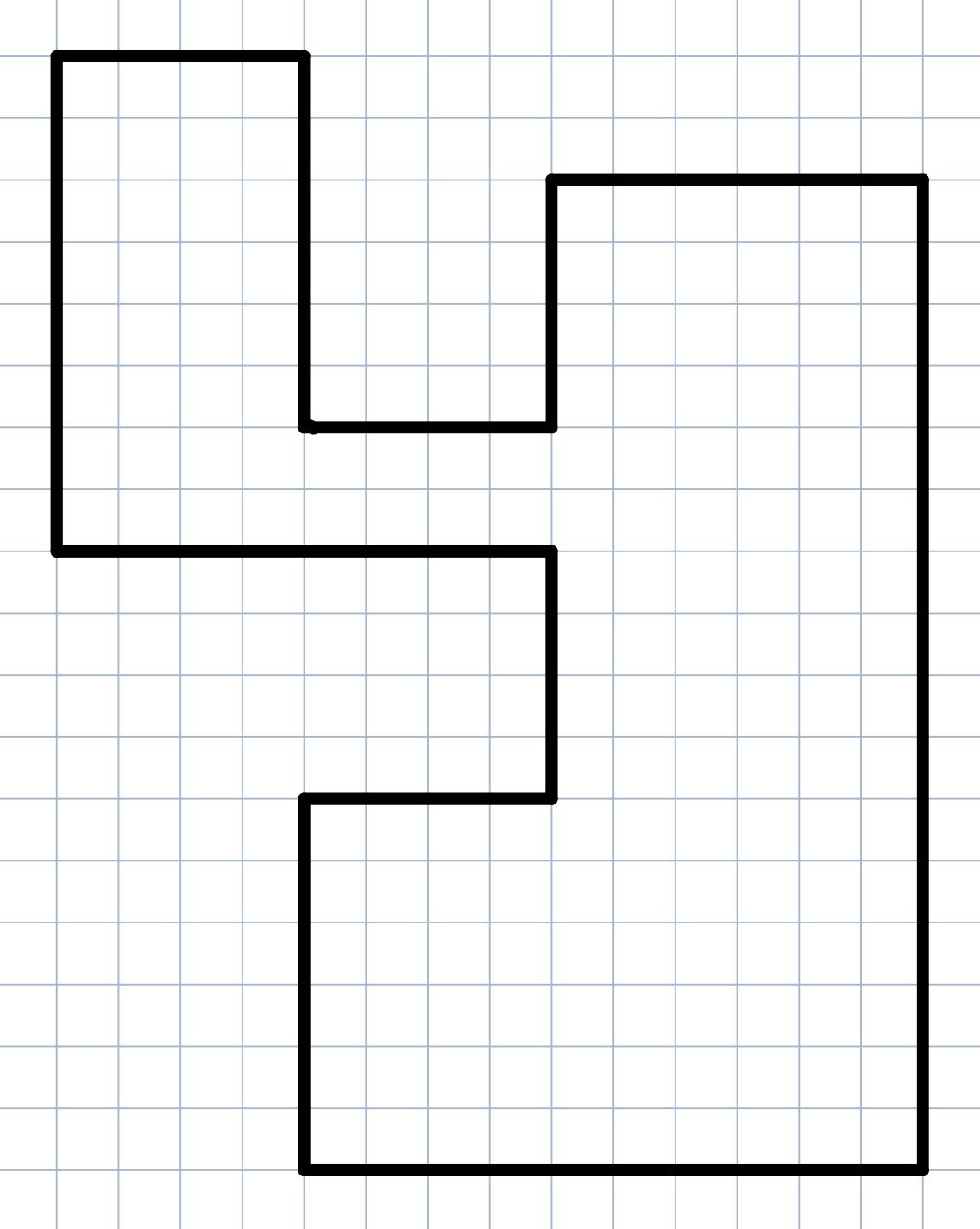
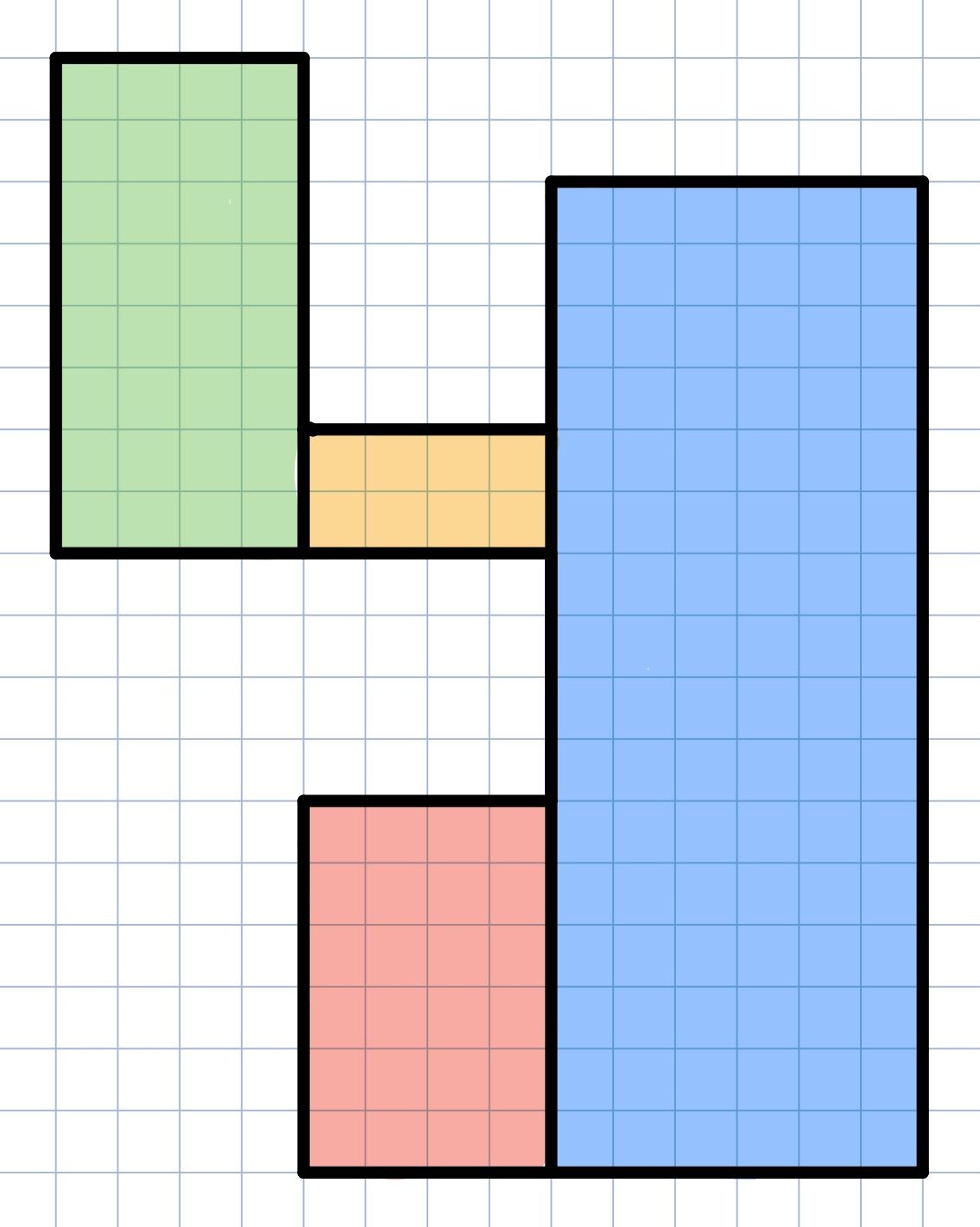
3. Berechne alle Teilflächen.

A_{(g r \overset{u}{¨} n)} = a \cdot b = 2 c m \cdot 4 c m = \underline{\underline{8cm²}}

A_{(g e l b)} = a \cdot b = 1 c m \cdot 2 c m = \underline{\underline{2cm²}}

A_{(b l a u)} = a \cdot b = 3 c m \cdot 8 c m = \underline{\underline{24cm²}}

A_{(ro t)} = a \cdot b = 2 c m \cdot 3 c m = \underline{\underline{6cm²}}

4. Berechne die Gesamtfläche des Zimmers.

A_{(g es am t)} = A_{(g r \overset{u}{¨} n)} + A_{(g e l b)} + A_{(b l a u)} + A_{(ro t)} = 8 c m^{2} + 2 c m^{2} + 24 c m^{2} + 6 c m^{2} = \underline{\underline{40cm²}}