HerunterladenAls PDF Herunterladen
  • Höhe, Mittelsenkrechte, Winkelhalbierende
  • MNWeG
  • 11.08.2023
  • Mathematik
  • Raum und Form
  • M (Mindeststandard)
  • 9
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Höhe, Mittelsenkrechte, Winkelhalbierende
Mathematik Raum und Form M 9
1
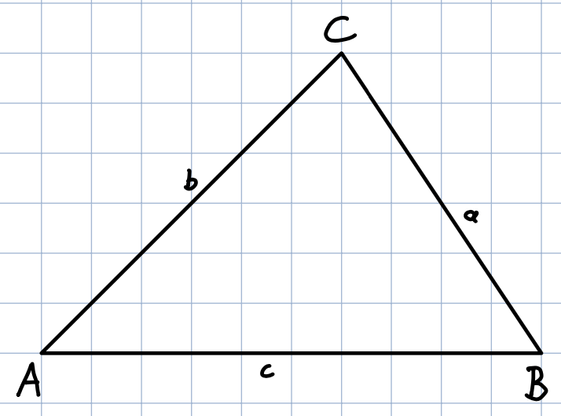
Über­tra­ge das Drei­eck auf ein ka­rier­tes Blatt.
Zeich­ne die Höhen in das Drei­eck ein.
Mar­kie­re den Schnitt­punkt S.
2
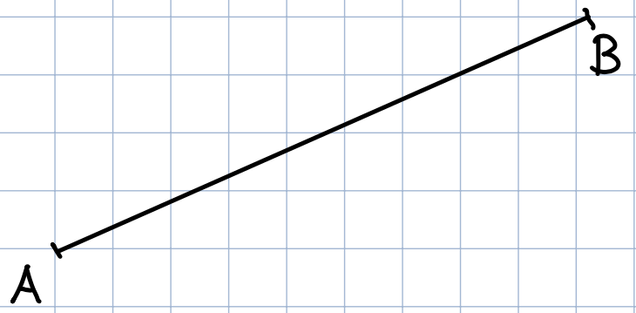
Über­tra­ge die Stre­cke auf ein ka­rier­tes Blatt.
Zeich­ne die Mit­tel­senk­rech­te in die Stre­cke ein.
Mar­kie­re den Schnitt­punkt M.
3
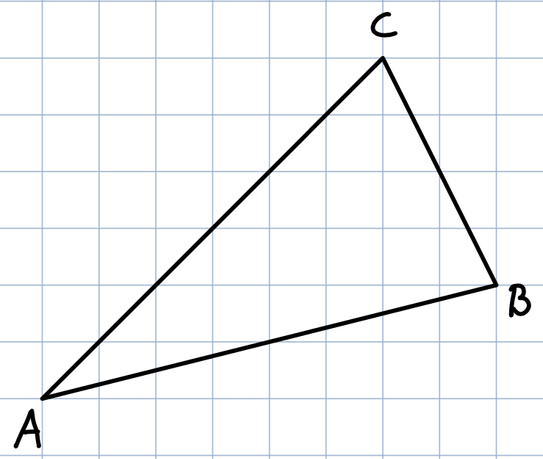
Über­tra­ge das Drei­eck auf ein ka­rier­tes Blatt.
Zeich­ne die Mit­tel­senk­rech­ten in das Drei­eck ein.
Mar­kie­re den Schnitt­punkt S.
Was fällt dir auf? Kannst du auch den Um­kreis ein­zeich­nen?
Bereitgestellt von: MNWeG Stand: 11.08.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/hoehe-mittelsenkrechte-winkelhalbierende-2
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/hoehe-mittelsenkrechte-winkelhalbierende-2
AB
Höhe, Mittelsenkrechte, Winkelhalbierende
Mathematik Raum und Form M 9
4
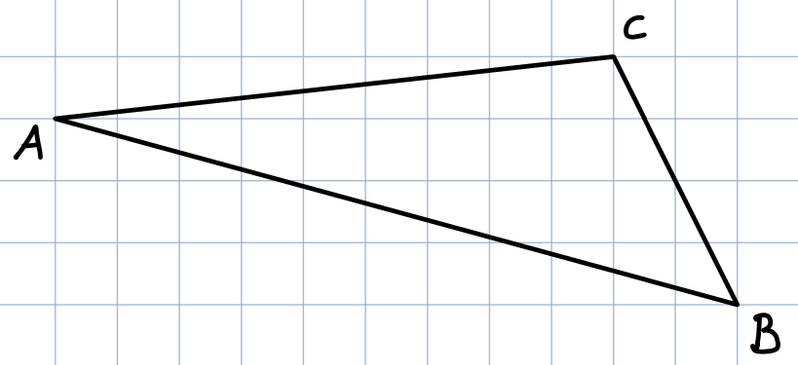
Über­tra­ge das Drei­eck auf ein ka­rier­tes Blatt.
Zeich­ne die Mit­tel­senk­rech­ten in das Drei­eck ein.
Mar­kie­re den Schnitt­punkt S.
Was fällt dir auf? Kannst du auch den Um­kreis ein­zeich­nen?
5
Über­tra­ge das Drei­eck auf ein ka­rier­tes Blatt.
Zeich­ne die Win­kel­hal­bie­ren­den in das Drei­eck ein.
Mar­kie­re den Schnitt­punkt S.
Was fällt dir auf? Kannst du auch den In­kreis ein­zeich­nen?
6
Über­tra­ge das Drei­eck auf ein ka­rier­tes Blatt.
Zeich­ne die Win­kel­hal­bie­ren­den in das Drei­eck ein.
Mar­kie­re den Schnitt­punkt S.
Was fällt dir auf? Kannst du auch den In­kreis ein­zeich­nen?
Bereitgestellt von: MNWeG Stand: 11.08.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/hoehe-mittelsenkrechte-winkelhalbierende-2
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/hoehe-mittelsenkrechte-winkelhalbierende-2
x