Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Körper zeichnerisch darstellen
Mathematik Raum und Form M 9
1
Zeichne die Netze der Quader auf ein kariertes Blatt.
Markiere gegenüberliegende Flächen in der gleichen Farbe.
Markiere gegenüberliegende Flächen in der gleichen Farbe.
Quader A
Quader B
2
Aufgabe zu einer quadratischen Pyramide.
- Zeichne das Netz einer quadratischen Pyramide, bei der die Seitenlänge der Grundfläche 3 cm beträgt und die Höhe der Dreiecke jeweils 5 cm.
- Berechne anschließend die Oberfläche und das Volumen der Pyramide.
3
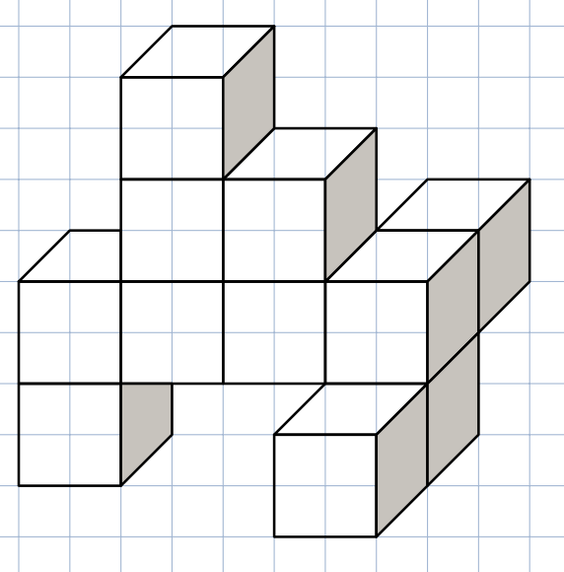
Hier siehst du ein Bauwerk, das aus vielen kleinen Würfeln zusammengesetzt ist.
Ergänze dieses Bauwerk zu dem kleinstmöglichen Quader, ohne Würfel umzubauen.
Wie viele kleine Würfel fehlen?
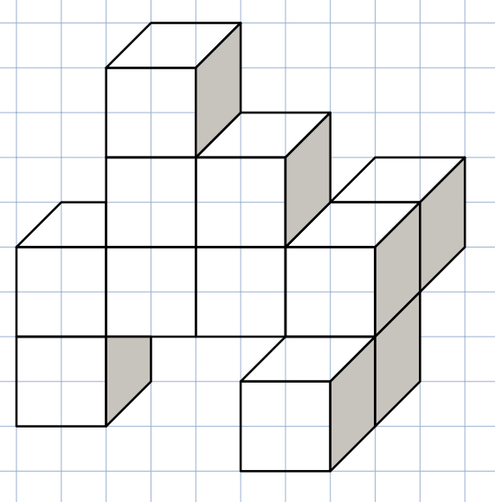
Ergänze dieses Bauwerk zu dem kleinstmöglichen Quader, ohne Würfel umzubauen.
Wie viele kleine Würfel fehlen?
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/koerper-zeichnerisch-darstellen-5
https://editor.mnweg.org/mnw/dokument/koerper-zeichnerisch-darstellen-5
AB
Körper zeichnerisch darstellen
Mathematik Raum und Form M 9
4
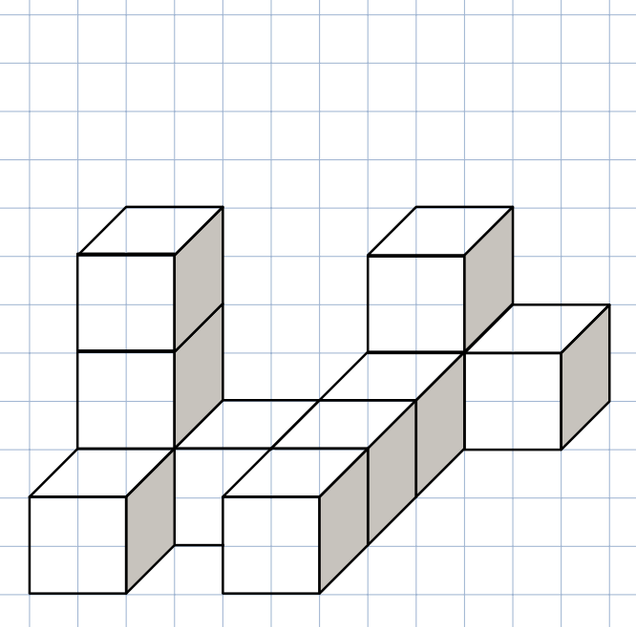
Hier siehst du ein Bauwerk, das aus vielen kleinen Würfeln zusammengesetzt ist.
Ergänze dieses Bauwerk zu dem kleinstmöglichen Würfel, ohne Würfel umzubauen.
Wie viele kleine Würfel fehlen?
Ergänze dieses Bauwerk zu dem kleinstmöglichen Würfel, ohne Würfel umzubauen.
Wie viele kleine Würfel fehlen?
Privat: A.Schöler
5
Zeichne ein Prisma, welches als Grundfläche ein gleichseitiges Dreieck hat.
Der Umfang des Dreieckes beträgt 12 cm, die Höhe des Prismas beträgt 5,8 cm.
Der Umfang des Dreieckes beträgt 12 cm, die Höhe des Prismas beträgt 5,8 cm.
6
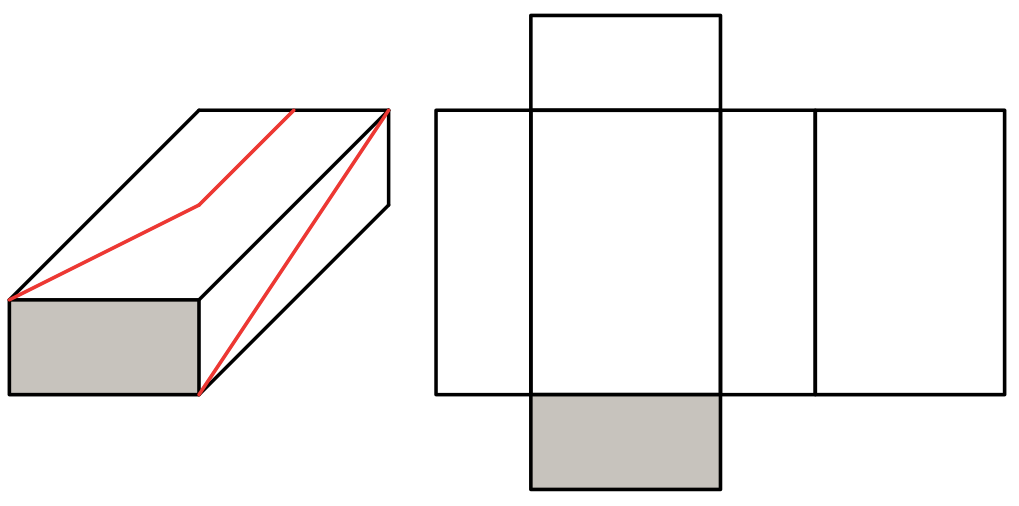
Übertrage die roten Strecken vom Quader auf das Netz. Es sind zwei Lösungen möglich.
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/koerper-zeichnerisch-darstellen-5
https://editor.mnweg.org/mnw/dokument/koerper-zeichnerisch-darstellen-5
AB
Körper zeichnerisch darstellen
Mathematik Raum und Form M 9
7
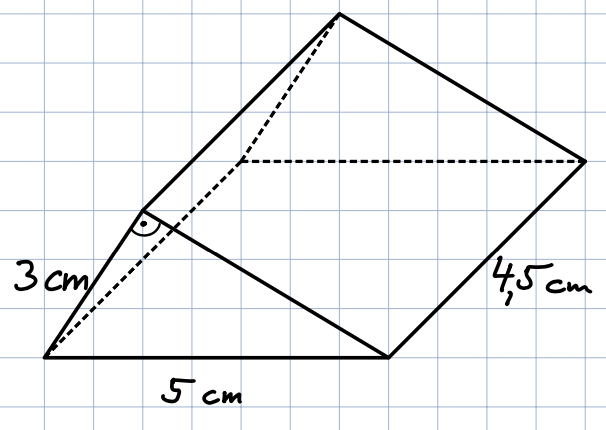
Zeichne das Netz des Dreiecksprismas mit den entsprechenden Angaben.
8
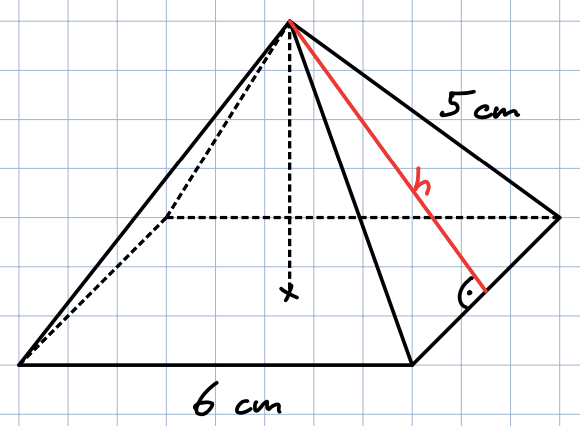
Quadratische Pyramide
- Zeichne das Netz der quadratischen Pyramide mit den entsprechenden Angaben.
- Wie viele cm beträgt die Gesamtlänge aller Kanten der Pyramide?
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/koerper-zeichnerisch-darstellen-5
https://editor.mnweg.org/mnw/dokument/koerper-zeichnerisch-darstellen-5


