Hier wurden die Zahlen mit Vorzeichen vertauscht (Kummatitivgesetz). Es kann trotzdem gekürzt werden.
Kürzen
Bruchterme können durch Kürzen vereinfacht werden. Dies ist wichtig, da vereinfachte
Bruchterme leichter zu verstehen und zu interpretieren sind. Dadurch können Brüche einfacher miteinander verglichen werden. Auch könnten komplizierte Brüche zu Rechenfehlern führen.
Beim Kürzen von Bruchtermen werden Zähler und Nenner durch die selbe Zahl oder Variable geteilt.
Beispiele:
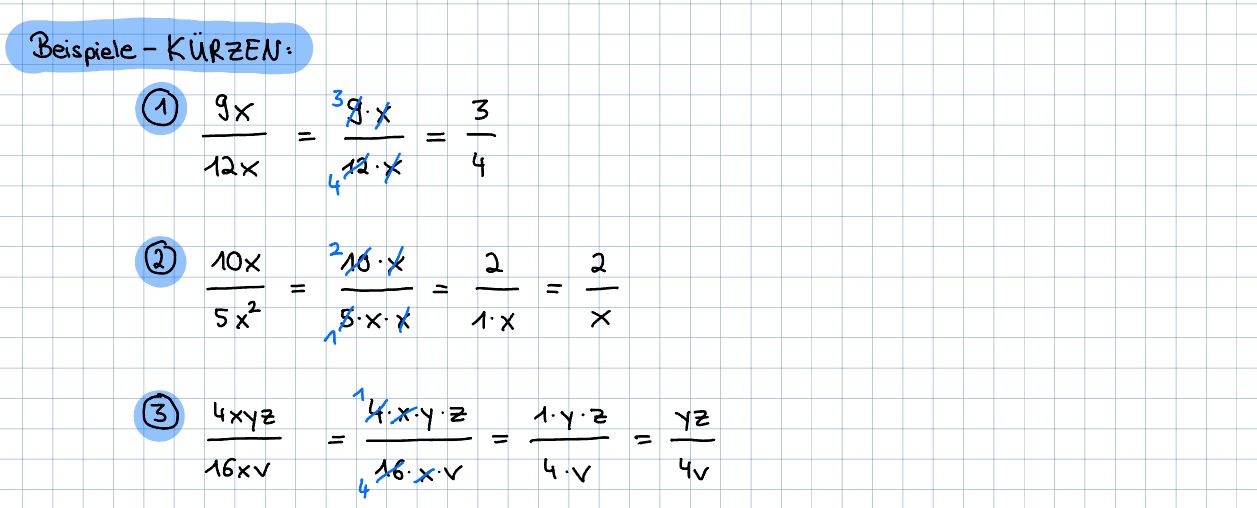
https://editor.mnweg.org/mnw/dokument/kuerzen-ausklammern-3
Ausklammern und Kürzen
Ausklammern bei Bruchtermen ist eine Technik, um Brüche zu vereinfachen, indem man einen gemeinsamen Faktor sowohl im Zähler als auch im Nenner findet und diesen dann ausklammert. Ausklammern wird deshalb auch Faktorisieren
genannt.
Betrachten wir den Bruchterm:
Schritte zum Ausklammern:
1. Faktor herausfinden:
Im Nenner haben beide Terme den gemeinsamen Faktor 4x.
2. Ausklammern:
4x wird im Nenner ausgeklammert:
3. Kürzen:
Jetzt können wir die gemeinsamen Faktoren im Zähler und im Nenner kürzen.
Zuerst kürzen wir x: Dann kürzen wir die 4 und 2:
Beispiele:
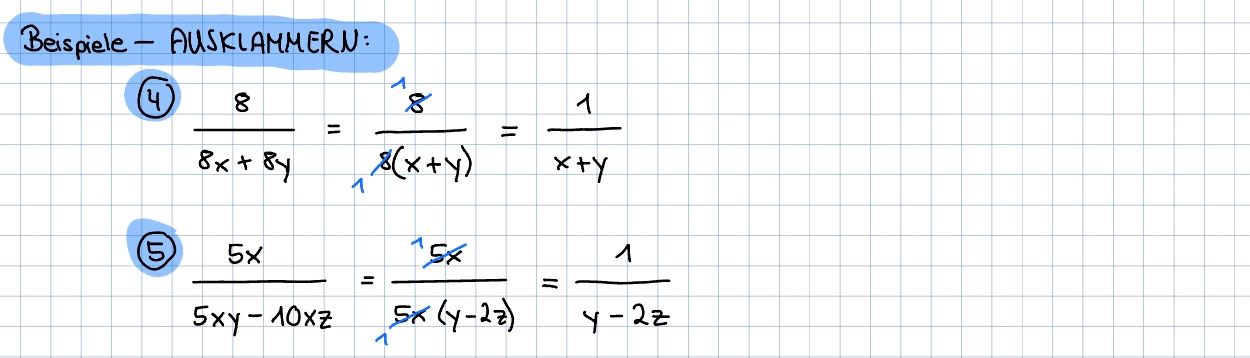

https://editor.mnweg.org/mnw/dokument/kuerzen-ausklammern-3
Ausklammern und Kürzen - SONDERFÄLLE
Beispiele:
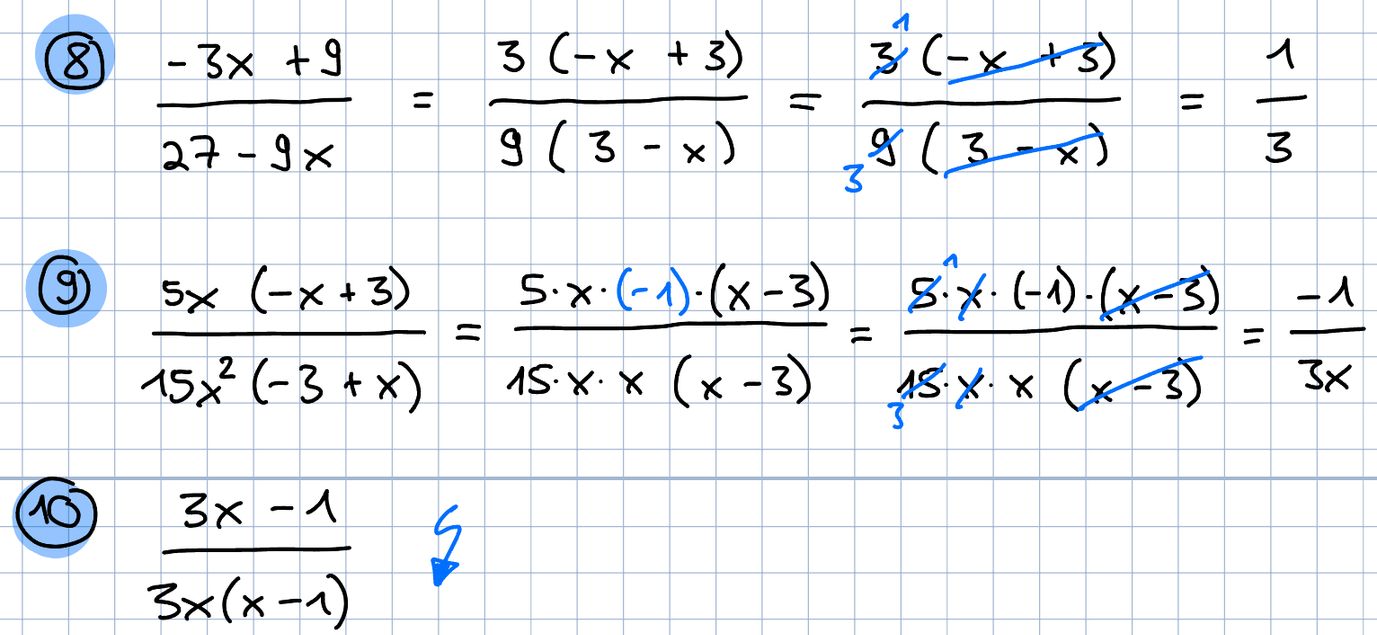
Hier kann (-1) ausgeklammert werden, damit dann die Terme gekürzt werden können.
Hier kann NICHT ausgeklammert und NICHT weiter gekürzt werden, da es sich um zwei verschiedene Terme handelt. Differenzen und Summen dürfen nicht gekürzt werden.
Kürze Terme nur, wenn diese als Ganzes stehen, denn
Aus Differenzen und Summen kürzen nur die Dummen.
https://editor.mnweg.org/mnw/dokument/kuerzen-ausklammern-3
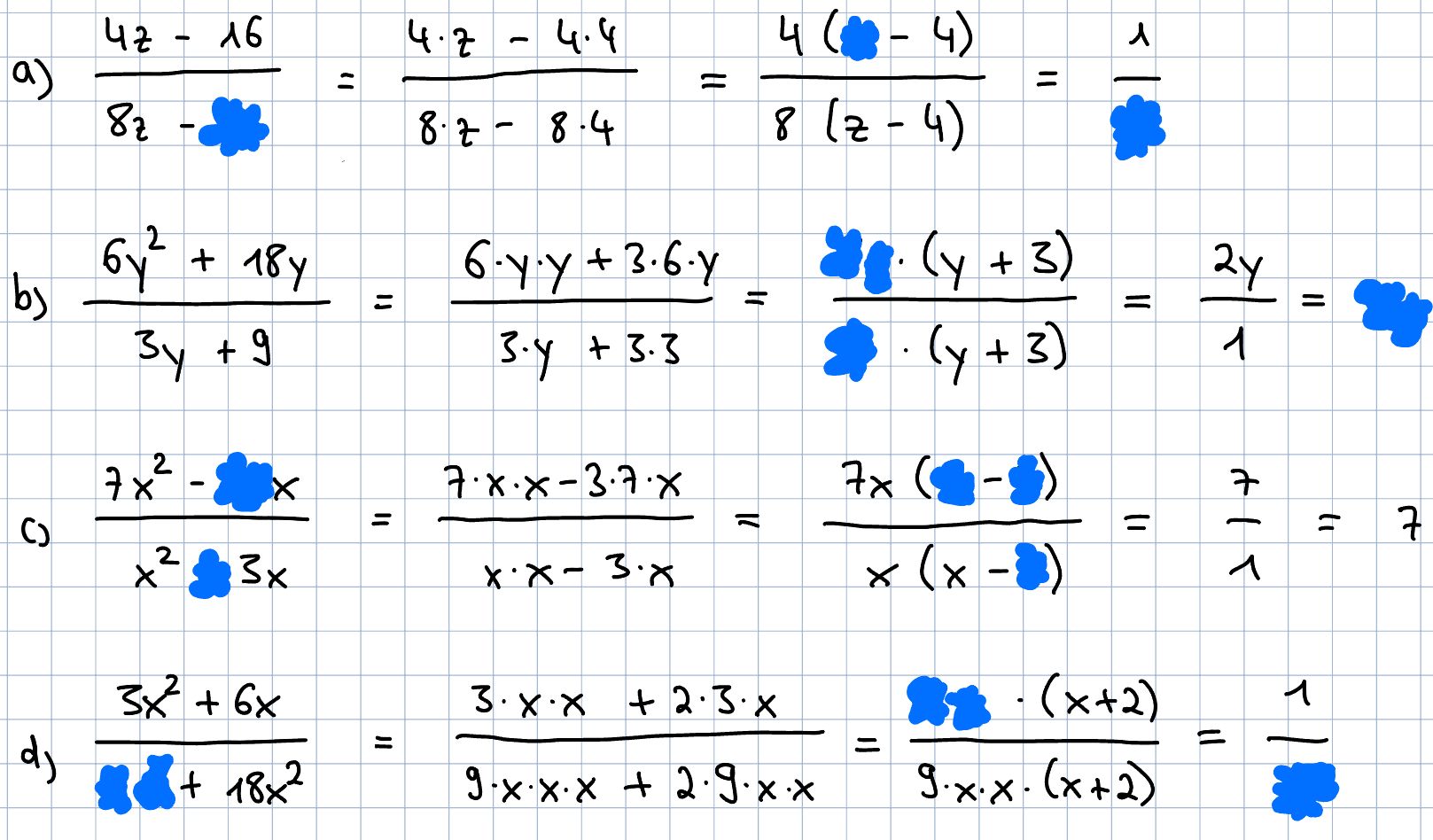
https://editor.mnweg.org/mnw/dokument/kuerzen-ausklammern-3


