Lineare Funktionen verstehen und lösen
Der Graph einer linearen Funktion ist immer eine Gerade.
Im Gegensatz zu einer proportionalen Zuordnung geht eine lineare Funktion jedoch nicht durch den Nullpunkt. Sonst wäre es ja eine proportionale Zuordnung.
- Die Funktionsgleichung lautet: f(x) = mx + c
- Die Steigung m gibt an, ob die Gerade steigt oder fällt
m 0 die Gerade steigt
m 0 die Gerade ist parallel zur x-Achse
m 0 die Gerade fällt
- Die Variable c (wird manchmal auch als b geschrieben) gibt den y-Achsenabschnitt an, an dem die Gerade die
y-Achse (y = c) schneidet.
Also z.B. c = 2 Schnittpunkt (0|2)
- Mit Hilfe des sogenannten Steigungsdreieckes kann man die Steigung einzeichnen.
- Lineare Funktionen können als Funktionsgleichung, in einer Wertetabelle oder als Graph dargestellt werden.
Mit dieser APP kannst du die linearen
Funktionen nochmals üben.
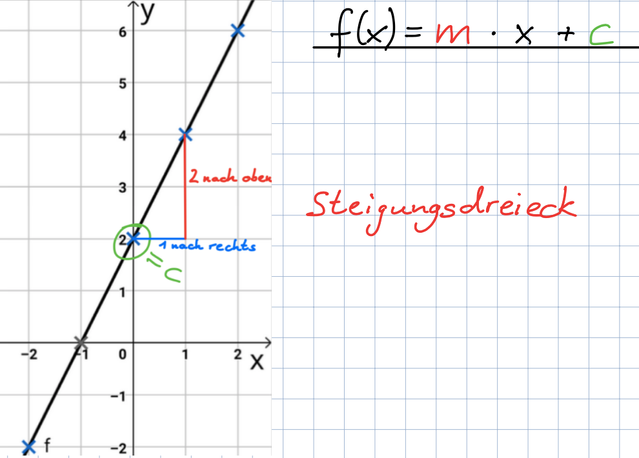
Hier siehst du den Graphen mit einem Steigungsdreieck. Überlege dir, welchen Wert c hat und wie groß die Steigung m ist. Schreibe die Funktionsgleichung auf.
Tipp: Lösung immer abdecken!
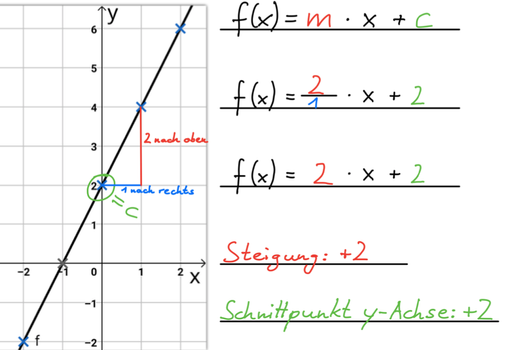
Ergänze die Wertetabelle. Die Funktionsgleichung lautet: f(x) = 2x + 2
x
0
1
2
3
4
5
f(x) = y
6
8
Hier siehst du einen weiteren Graphen. Überlege dir, welchen Wert c hat und wie groß die Steigung m ist. Zeichne das Steigungsdreieck ein und schreibe die Funktionsgleichung auf.
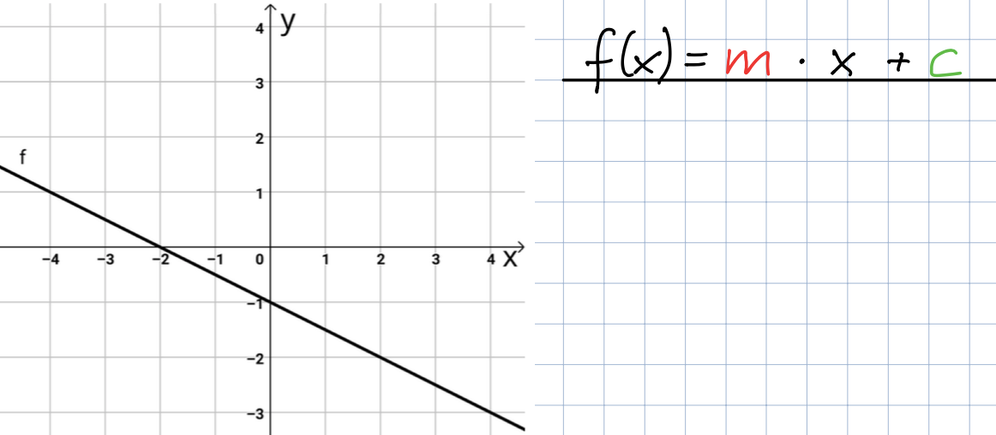
Hier siehst du drei verschiedene Graphen.
Schreibe den richtigen Buchstaben in die Tabelle
vor die jeweilige Funktion.
Zur Übung kannst du auch nochmal die Steigungsdreiecke einzeichnen.
Die Steigung findest du, indem
du von einem zum nächsten
Kästchenschnittpunkt gehst.
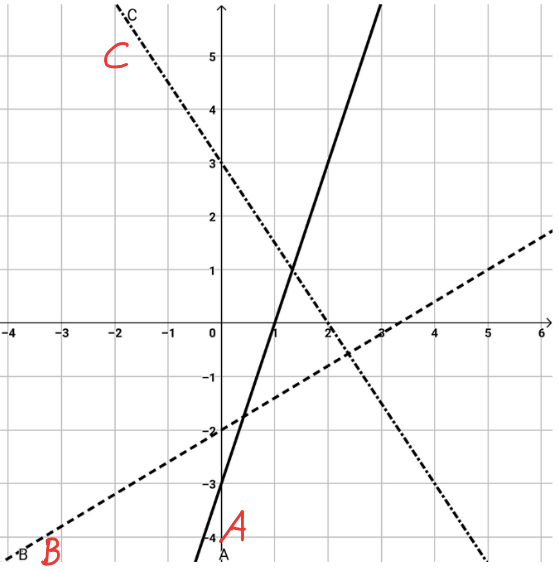
f(x) = x - 2 oder f(x) = 0,6 x - 2
f(x) = - x + 3 oder f(x) = - 1,5 x + 3
f(x) = 3x - 3
Ergänze die Wertetabelle. Die Funktionsgleichung lautet: f(x) = - x - 1
x
- 3
- 2
- 1
0
1
2
3
f(x) = y
