Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
1
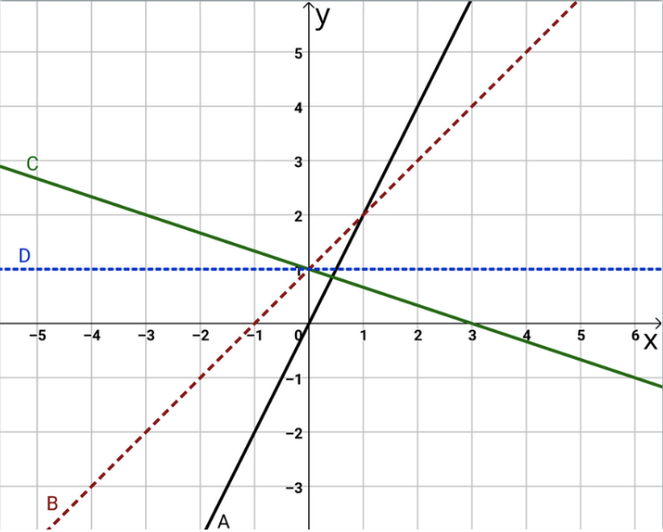
Schreibe die Funktionsgleichungen für A und B auf.
Denke an das Steigungsdreieck.
Denke an das Steigungsdreieck.
Tipp
Die Steigung findest du, indem
du von einem zum nächsten
Kästchenschnittpunkt gehst.
2
Zeichne einen Graphen zu der Funktionsgleichung f(x) = - 0,5 x - 1 für die x-Werte - 4 bis + 4.
Tipp: Es genügt, wenn du zwei Punkte berechnest. Am besten keine Nachbarpunkte!
Tipp: Es genügt, wenn du zwei Punkte berechnest. Am besten keine Nachbarpunkte!
3
Welcher Buchstabe gehört zu welcher Funktion?
Schreibe den richtigen Buchstaben in die Tabelle vor die Funktion.
Schreibe den richtigen Buchstaben in die Tabelle vor die Funktion.
f(x) = 2 x
f(x) = - x + 1
f(x) = 1
f(x) = x + 1
4
Welcher Buchstabe gehört zu welcher Funktion?
Schreibe den richtigen Buchstaben in die Tabelle vor die Funktion. Ergänze am Ende die fehlende Funktion.
Schreibe den richtigen Buchstaben in die Tabelle vor die Funktion. Ergänze am Ende die fehlende Funktion.
f(x) = x + 3
f(x) = - 3
f(x) = 4 x - 1
5
Ergänze die Wertetabelle. Die Funktionsgleichung lautet: f(x) = - 2x + 1,5
x
- 2
- 1
0
1
2
3
f(x) = y
- 0,5
6
In Tiengen kannst du von verschiedenen Anbietern
einen E-Roller ausleihen. In der entsprechenden APP
findest du drei unterschiedliche Angebote.
Welches Angebot würdest du wählen, wenn du im Monat die E-Roller etwa 125 Minuten nutzen würdest?
einen E-Roller ausleihen. In der entsprechenden APP
findest du drei unterschiedliche Angebote.
Welches Angebot würdest du wählen, wenn du im Monat die E-Roller etwa 125 Minuten nutzen würdest?
Angebot A
Gesamtkosten incl. 100 Min./Monat
40 €
jede weitere
Minute 50 Cent
Angebot B
Grundgebühr
15 €/Monat
Preis pro
Minute 35 Cent
Angebot C
Keine
Grundgebühr
Preis pro
Minute nur
45 Cent
