Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
1
Finde die Lösung der Platzhalter, wenn möglich im Kopf.
- 7 = 14
- 6 = 60
- 10 = 30
- 4 + 4 =
- 5 = 10
- 9 9 =
- 4 + 5 =
- 1 2 =
2
Berechne die folgenden Terme und achte auf die allgemeine Rechenregel.
- 2 + 3 2 =
- 7 (9+2) =
- 5 (+9) = 55
- 4 (+6) = 28
- 7 + 8 3 =
- 2 + 9 = 65
- 10 + 7 = 59
- 4 (2+7) =
- 6 + 2 5 =
Es gilt immer: Klammer vor Punkt vor Strich!
Ich kann bei Termen die Grundrechenarten durchführen.
Unbekannte Gesamtlänge darstellen.
Du kannst eine gesamte Länge oder einen Umfang einer Fläche auch mit Termen darstellen. Ordne jedem einfach eine Variable zu. Gleiche Abschnitte erhalten hierbei die gleichen Variablen. Danach kannst du diese Variablen zusammen als Term aufschreiben.
Gleichem Abschnitt gleiche Variable zuordnen:
Term aufschreiben:
Definiere für die Abschnitte entsprechende Variablen. Schreibe anschließend die Gesamtlänge als Terme auf. (Du darfst selber entscheiden, welche Variable du für welche Form verwendest.)
3
Richtung der Striche
Es ist egal, in welche Richtung die Striche zeigen. Du "läufst" die Strecke entlang. Also rechnest du immer jeden weiteren Abschnitt mit + dazu.
4
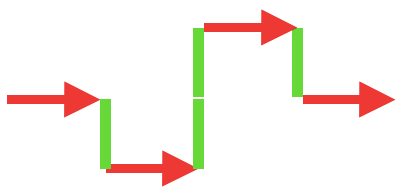
5
6
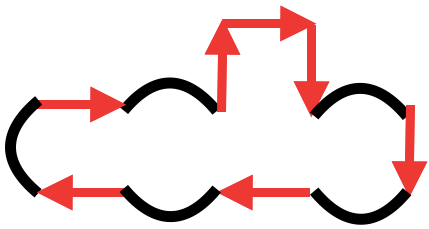
7
8
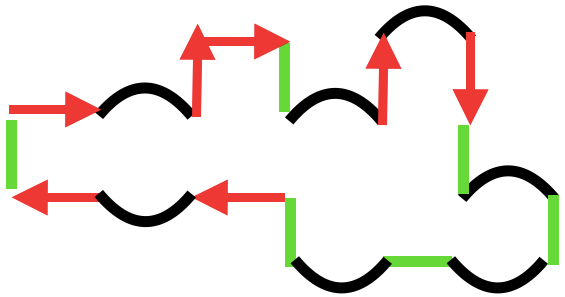
9
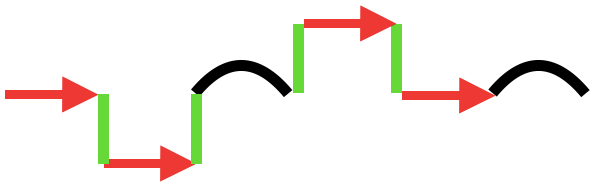
10
