Die Mittelsenkrechte
Die Mittelsenkrechte schneidet eine Strecke genau senkrecht in deren Mitte im Punkt M.
Diese Mittelsenkrechte m geht durch den Punkt M.
Am Beispiel der Strecke kannst du die
eingezeichnete Mittelsenkrechte m sehen.
Einfach die Streckenlänge messen und halbieren.
Die drei Mittelsenkrechten in einem Dreieck schneiden sich in einem Punkt. Damit kannst du deine Lösung ganz einfach kontrollieren.
Der Schnittpunkt kann auch außerhalb des Dreieckes liegen (bei einem stumpfwinkligen Dreieck).
Wenn du mit einem Zirkel einen Kreis um den Punkt S zeichnest, dann schneidet die Kreislinie alle drei Eckpunkte des Dreieckes.
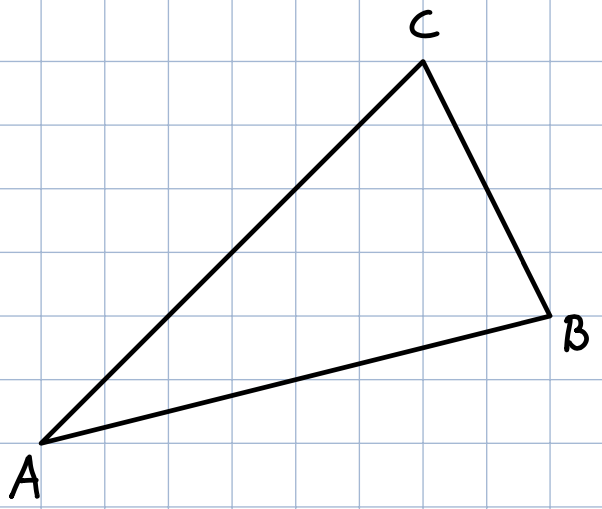
- Übertrage das Dreieck auf ein kariertes Blatt.
- Zeichne die drei Mittelsenkrechten in das Dreieck ein.
- Markiere den Schnittpunkt S.
- Zeichne den Umkreis durch die Eckpunkte.
Die Winkelhalbierende
Die Winkelhalbierende halbiert, wie der Name schon sagt, einen gegebenen Winkel.
Wenn ein Winkel α z.B. 48° hat, dann müsstest du einen Winkel mit 24° als Winkelhalbierende
einzeichnen.
Die drei Winkelhalbierenden in einem Dreieck schneiden sich in einem Punkt. Damit kannst du deine Lösung ganz einfach kontrollieren.
Beispiel:
Der Winkel α ist 70°. Die Hälfte von α ist also 35° = α1.
Dieser Winkel wird an einem der zwei Schenkel eingetragen.
- Übertrage das Dreieck auf ein kariertes Blatt.
- Zeichne die drei Winkelhalbierenden in das Dreieck ein.
- Markiere den Schnittpunkt S.
- Zeichne den Inkreis. Dieser berührt alle drei Seiten des Dreieckes.
Wenn du mit einem Zirkel einen Kreis um den Punkt S zeichnest, dann berührt die Kreislinie alle
drei Seiten des Dreieckes.
