HerunterladenAls PDF Herunterladen
  • Oberflächen/Rauminhalte Wü., Quad., Pris.
  • MNWeG
  • 10.01.2024
  • Mathematik
  • Messen
  • M (Mindeststandard)
  • 9
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Oberflächen/Rauminhalte Wü., Quad., Pris.
Mathematik Messen M 9

Ober­flä­chen und Raum­in­hal­te von Wür­feln und Pris­men

Teil A1 - Auf­ga­ben

OHNE Ta­schen­rech­ner

Re­chen­weg

Um die volle Punkt­zahl zu er­hal­ten, soll­test du beim Lösen der Auf­ga­ben stets den Re­chen­weg an­ge­ben, d.h. ...

- For­mel auf­schrei­ben,

- Zah­len in die For­mel ein­set­zen,

- rech­nen und

- Lö­sung dop­pelt un­ter­strei­chen.

1
Ein Qua­der hat die Kan­ten­län­gen a = 2 cm,
b = 4 cm und c = 6 cm.
Be­rech­ne das Vo­lu­men und die Ober­flä­che des Qua­ders.
2
Das oben of­fe­ne Aqua­ri­um der Schild­krö­ten im grü­nen
Lern­haus ist 1 m breit, 60 cm tief und 50 cm hoch.
Die Was­ser­hö­he be­trägt 15 cm.
  • Wie viel Liter Was­ser sind im Aqua­ri­um?
  • Wie groß ist die Glas­flä­che des Aqua­ri­ums?
3
Alle Kan­ten eines Wür­fels sind zu­sam­men 60 cm lang.
  • Wie lang ist eine Kante?
  • Wie groß ist Ober­flä­che des Wür­fels?
  • Wie groß ist das Vo­lu­men des Wür­fels?
4
Das Vo­lu­men eines Qua­ders be­trägt 112 cm3. Die qua­dra­ti­sche Sei­ten­flä­che hat eine
Sei­ten­län­ge von 4 cm.
Be­rech­ne die Ober­flä­che des Qua­ders.
Tipp: Die feh­len­de Sei­ten­län­ge be­kommst du über das Vo­lu­men her­aus. Am Bes­ten fer­tigst du dazu eine Skiz­ze an.
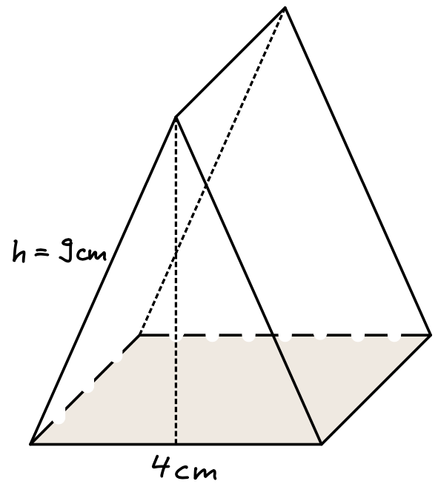
5
Be­rech­ne das Vo­lu­men des ab­ge­bil­de­ten Haus­da­ches mit einer qua­dra­ti­schen Grund­flä­che.
Bereitgestellt von: MNWeG Stand: 10.01.2024 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/oberflaechenrauminhalte-wue-quad-pris-5
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/oberflaechenrauminhalte-wue-quad-pris-5
AB
Oberflächen/Rauminhalte Wü., Quad., Pris.
Mathematik Messen M 9

Teil A2/B - Auf­ga­ben

MIT Hilfs­mit­teln wie TR und For­mel­samm­lung.

6
Nach­ge­dacht
  • Wie ver­än­dert sich das Vo­lu­men, wenn die Sei­ten­län­gen eines Qua­ders ver­dop­pelt wer­den?

  • Wie ver­än­dert sich die Ober­flä­che, wenn die Sei­ten­län­gen eines Qua­ders ver­dop­pelt wer­den?
    Tipp: Am Bes­ten fer­tigst du eine Skiz­ze oder wen­dest die For­mel an.
7
Du hast einen Wür­fel mit einer Ober­flä­che von 37,5 cm2 vor dir lie­gen.
  • Wie lang ist eine Kante des Wür­fels?

  • Wie groß ist der Raum­in­halt (das Vo­lu­men) des Wür­fels?
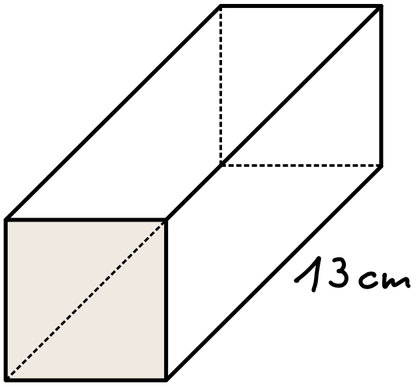
8
Der ab­ge­bil­de­te Qua­der mit einer qua­dra­ti­schen Flä­che
hat eine Ge­samt­kan­ten­län­ge von genau 100 cm.
Be­rech­ne das Vo­lu­men des Qua­ders.
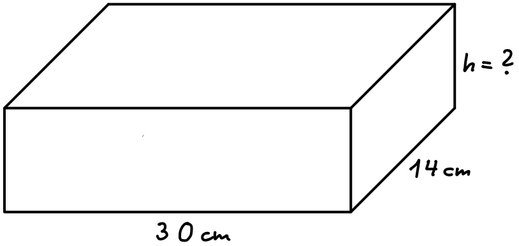
9
Der ab­ge­bil­de­te Qua­der hat ein Vo­lu­men von 6.300 cm3.
Be­rech­ne die Höhe des Qua­ders.
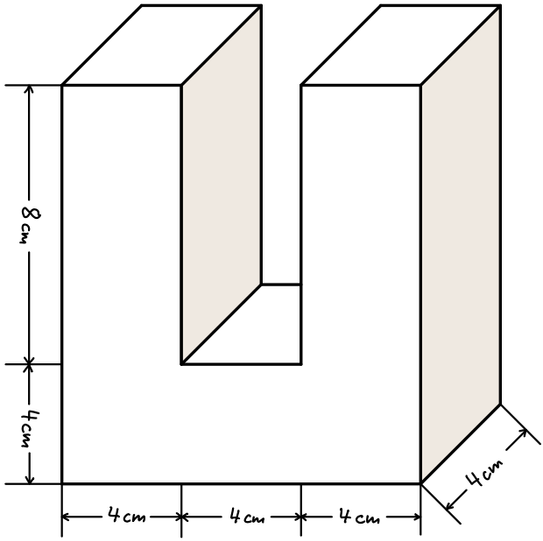
10
Hier siehst du ein gro­ßes U.
  • Wie groß ist das Vo­lu­men des Buch­sta­bens?
    Tipp: Zeich­nung zu­erst genau an­schau­en und über­le­gen.
    Viel­leicht kannst du den Buch­sta­ben ja zer­le­gen!?

  • Wie groß ist die Ober­flä­che des Buch­sta­bens?
    Auch hier zu­erst genau über­le­gen.
Bereitgestellt von: MNWeG Stand: 10.01.2024 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/oberflaechenrauminhalte-wue-quad-pris-5
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/oberflaechenrauminhalte-wue-quad-pris-5
x