Der Rauminhalt wird oft auch Volumen genannt.
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Oberflächen und Rauminhalte von Zylindern
Zylinder finden wir auf Wiesen und Feldern oder auf den Köpfen von vornehmen Herren.
Auch viele Verpackungen haben eine zylindrische Form, z.B. Dosen.
Achte mal bei deinem nächsten Einkauf darauf.
Schaue dir nun die beiden Videos an.
Wenn du die Aufgabe mit der Formel gleich mitschreibst,
bleibt es dir besser im Gedächtnis.
1
Überlege dir, wie die Formel für das Volumen und die Oberfläche eines Zylinders aussehen könnte.
Hinweis: Trage für das Volumen ein VZy ein und für die Oberfläche ein OZy.
Kannst du auch den anderen Formeln die Formelzeichen zuordnen?
Hinweis: Trage für das Volumen ein VZy ein und für die Oberfläche ein OZy.
Kannst du auch den anderen Formeln die Formelzeichen zuordnen?
- = a · b · c
- = π r2 · h
- = a · a · a
- = 2 π r2 + 2 π r · h
Oberfläche Zylinder
OZy = 2·G + M (M=Mantel)
OZy = 2 π r2 + 2 π r h
Lösung 1:
Volumen Zylinder
VZy = G · h = 2 π r2 · h
2
Beispiel: Volumen und Oberfläche eines Zylinders berechnen
Ein Zylinder hat den Radius r = 3 cm und eine Höhe h = 5 cm.
Berechne das Volumen und die Oberfläche des Zylinders.
Ein Zylinder hat den Radius r = 3 cm und eine Höhe h = 5 cm.
Berechne das Volumen und die Oberfläche des Zylinders.
Der Rauminhalt wird oft auch Volumen genannt.
Oberflächen und Rauminhalte von Pyramiden
Gizeh - Die Großen Pyramiden von Ägypten kennst du sicher.
Pyramiden sind oft beeindruckende Bauwerke aus der Vergangenheit. Es gibt aber auch neue Bauwerke, die uns beeindrucken, wie z.B. der Louvre in Paris.
Schaue dir nun das Video an
und schreibe die Formeln
gleich mit auf.
Louvre Museum in Paris
Oberfläche quadratische Pyramide
OPy = AQuadrat + 4 · ADreieck
OPy = a2 + 2 · a · hs (siehe Abb.)
(Anmerkung 4 · 0,5 = 2)
Volumen quadratische Pyramide
VPy = a2 · h
3
Beispiel: Volumen und Oberfläche einer Pyramide berechnen
Eine Pyramide hat die Seitenlänge a = 4 cm und die Höhe 5 cm.
Die Höhe der Dreiecksfläche hs beträgt 6 cm.
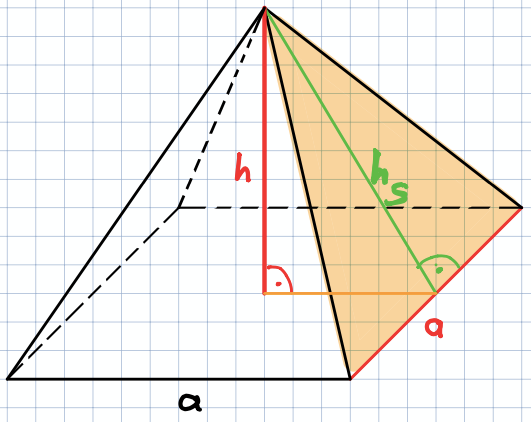
Eine Pyramide hat die Seitenlänge a = 4 cm und die Höhe 5 cm.
Die Höhe der Dreiecksfläche hs beträgt 6 cm.
Oberflächennetz einer
quadratischen Pyramide
Grundfläche: G = a · a = a2
Mantelfläche: M = 4 · Dreieck
= 4 · = 2 · a · hs
Oberflächenberechnung
Die Berechnung der Oberfläche ist eigentlich ganz logisch.
Der Mantel
der Pyramide besteht immer aus Dreiecken und die Grundfläche meist aus einem Quadrat.
Also: OPy = a · a + 4 · = a2 + 4 ·
