Der Rauminhalt wird oft auch Volumen genannt.
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Oberflächen und Rauminhalte von Zylindern und Pyramiden
Teil A2/B - Aufgaben
MIT Hilfsmitteln wie TR und Formelsammlung.
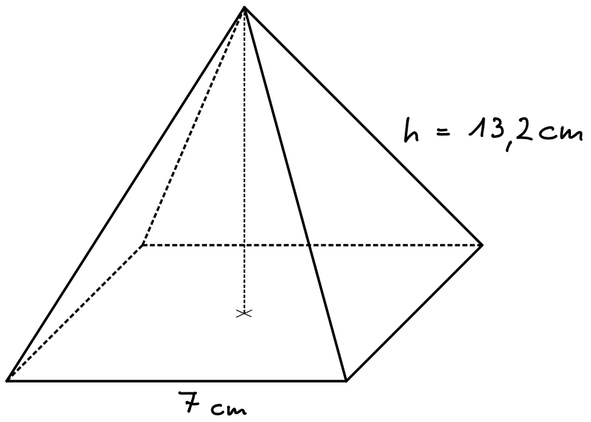
1
Berechne das Volumen der quadratischen Pyramide.
Ägypten 1999 (625) Kairo: Pyramiden von Gizeh
2
Das Volumen einer der drei quadratischen Cheops-Pyramiden in Ägypten beträgt 2.459.850 m3.
Die Seitenlänge des Quadrates beträgt 230 m.
Wie hoch ist die Pyramide?
Die Seitenlänge des Quadrates beträgt 230 m.
Wie hoch ist die Pyramide?
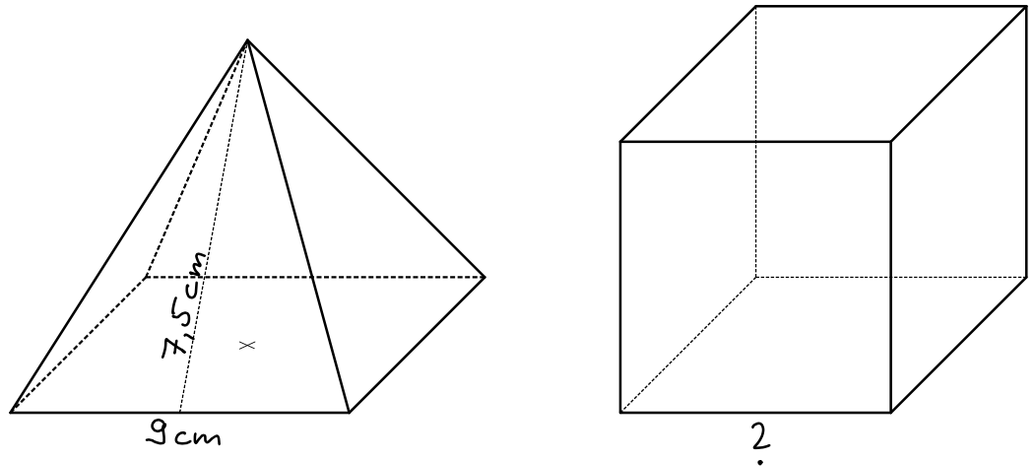
3
Die Oberflächen der quadratischen
Pyramide und des Würfels sind gleich groß.
Wie lang ist eine Kante des Würfels?
Pyramide und des Würfels sind gleich groß.
Wie lang ist eine Kante des Würfels?
Litfasssäule
4
Eine Säule soll mit einer Werbebanderole umklebt werden.
Die Höhe der Säule beträgt 2,8 m. Der Durchmesser beträgt 85 cm.
Welche Fläche muss die Werbebanderole haben, um die Säule zu umschließen?
Runde das Ergebnis sinnvoll.
Die Höhe der Säule beträgt 2,8 m. Der Durchmesser beträgt 85 cm.
Welche Fläche muss die Werbebanderole haben, um die Säule zu umschließen?
Runde das Ergebnis sinnvoll.
5
Es werden zwei Größen von Getränkedosen zum Verkauf
angeboten.
Die Dose A hat einen Durchmesser von 6,2 cm und eine
Höhe von 15 cm,
die Dose B hat einen Durchmesser von 5,8 cm und eine
Höhe von 16 cm.
angeboten.
Die Dose A hat einen Durchmesser von 6,2 cm und eine
Höhe von 15 cm,
die Dose B hat einen Durchmesser von 5,8 cm und eine
Höhe von 16 cm.
- Berechne für welche Dose weniger Blech benötigt wird.
- Wie groß ist der prozentuale Unterschied von Dose A zu B?
Du darfst dazu auf den Einer runden.
Getränkedosen
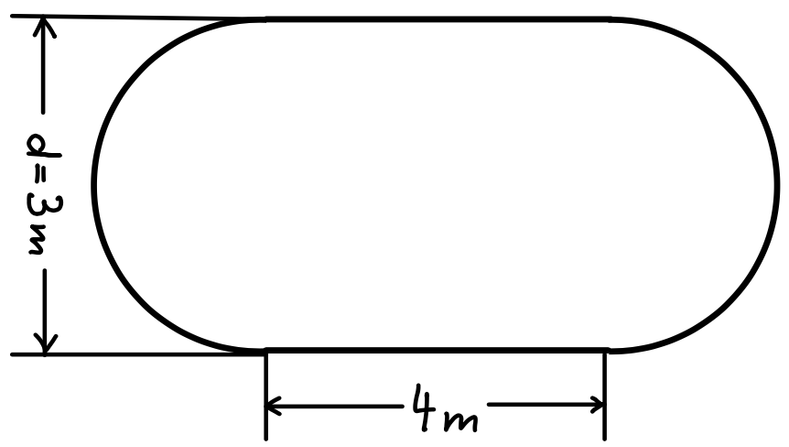
6
Hier siehst du ein Wasserbecken von oben.
Das Becken ist 2 m tief und zu 85 % gefüllt.
Das Becken ist 2 m tief und zu 85 % gefüllt.
- Wie viel Kubikmeter Wasser (m3) sind im Becken?
- Das Becken soll innen gestrichen werden.
Für wie viel Quadratmeter Innenfläche
muss Farbe gekauft werden?
