Prozentsätze in Säulen- und Streifendiagrammen darzustellen ist ganz einfach.
Wie es geht, erfährst du hier.
Kurze Wiederholung aus Statistik M 6
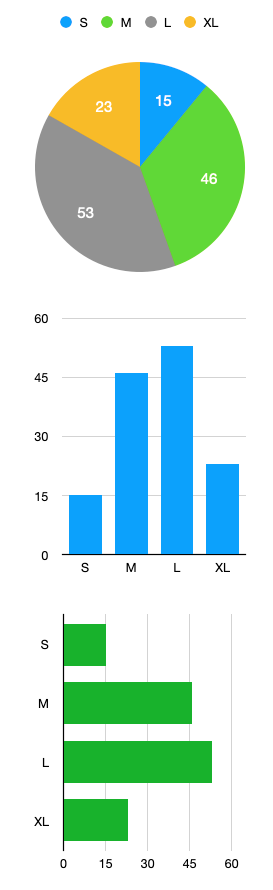
Das Säulendiagramm besteht aus zwei Achsen. Die Balken wachsen von unten nach oben - eben wie Säulen.
Das Streifendiagramm besteht aus einem Streifen, der in unterschiedliche Teile eingeteilt wird. Der ganze Streifen stellt meist genau 100% dar.

Prozentsätze in Säulendiagramm
Prozente werden meist auf den Grundwert 100 bezogen - daher ja auch der Name Pro-zent (von Hundert
oder Hundertstel
). Addiert man also alle Prozentsätze einer Datenreihe, dann erhält man als Ergebnis (normalerweise) genau 100%.
Bei einem Säulendiagramm musst du nun auf der x-Achse nur die Kategorien eintragen, und auf der y-Achse eine passende Skala von Prozenten. Beträgt bspw. der größte Anteil 47%, dann macht eine Skala bis 50% Sinn. Wenn du die Schritte von 10% in einem Abstand von 1cm einzeichnest, dann entspricht 1mm genau 1%.
Prozent
Kategorien
https://editor.mnweg.org/mnw/dokument/prozentsatze-in-diagrammen-1
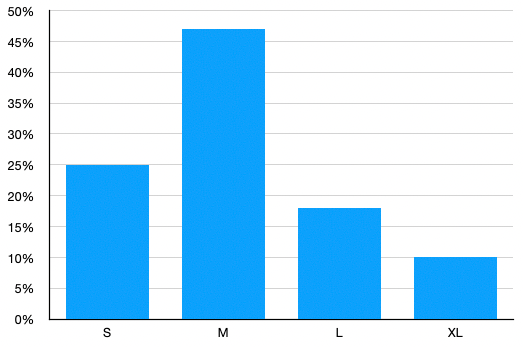
Beispiel:
Hier ist eine Datenreihe zu den Kleidergrößen in einer Lerngruppe:
S
M
L
XL
25%
47%
18%
10%
Zeichne ein Koordinatensystem und trage auf der x-Achse die Kategorien (hier Kleidergrößen), und auf der y-Achse eine passende Skala von Prozenten ein.
Da in diesem Beispiel der größte Prozentsatz 47% beträgt, macht eine Skala bis 50% Sinn.
Zeichne die %-Skala so ein, dass 10% genau 1cm enstpricht.
Trage nun die Werte entsprechend ein. Hierzu kannst du mit dem Lineal die Prozentwerte genau abmessen, da ja 1% genau 1mm entspricht.
FERTIG!
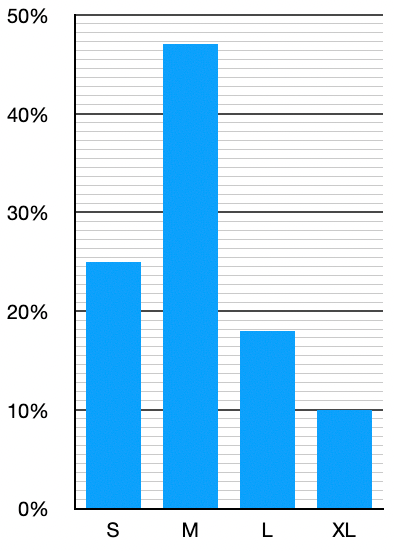
47%=∧47mm
https://editor.mnweg.org/mnw/dokument/prozentsatze-in-diagrammen-1
Prozentsätze in Streifendiagramm
Auch hier gilt: Prozente werden meist auf den Grundwert 100 bezogen - daher ja auch der Name Pro-zent (von Hundert
oder Hundertstel
). Addiert man also alle Prozentsätze einer Datenreihe, dann erhält man als Ergebnis (normalerweise) genau 100%.
Am einfachsten erstellt man ein Streifendiagramm, indem man von einem Streifen mit 10cm Länge ausgeht. Denn: 10cm sind genau 100mm. Und wenn alle Werte zusammen genau 100% ergeben, kann man pro 1% genau 1mm innerhalb des Streifens farblich markieren.
Um die Prozentsätze in mm umzurechnen, verwendet man am einfachsten einen Dreisatz.
Beispiel:
Nehmen wir als Beispiel wieder die Kleidergrößen:
S
M
L
XL
25%
47%
18%
10%
Dreisatz:
Zeichne nun einen Streifen mit 10cm bzw. 100mm Länge und trage die Teilabschnitte mit Hilfe eines Lineals in diesen Streifen ein.
25mm
47mm
18mm
10mm
https://editor.mnweg.org/mnw/dokument/prozentsatze-in-diagrammen-1


