TitelPunkt vor Strich
AutorMNWeG
veröffentlicht05.03.2021
FachMathematik
KompetenzbereichRechnen
NiveaustufeM (Mindeststandard)
Phase5
MaterialformInformation

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Die Regel

Die Regel "Punkt vor Strich" bedeutet, dass man innerhalb einer Rechnung immer zuerst die Punktrechnungen (also ﹒und ÷) berechnen muss, bevor man die Strichrechnungen (also + und -) berechnen kann.

Punkt vor Strich

Aber warum ist das wichtig?

Dass diese Regel in der Mathematik ganz wichtig ist, sieht man am besten, wenn man sich einmal ein Beispiel dazu ansieht.

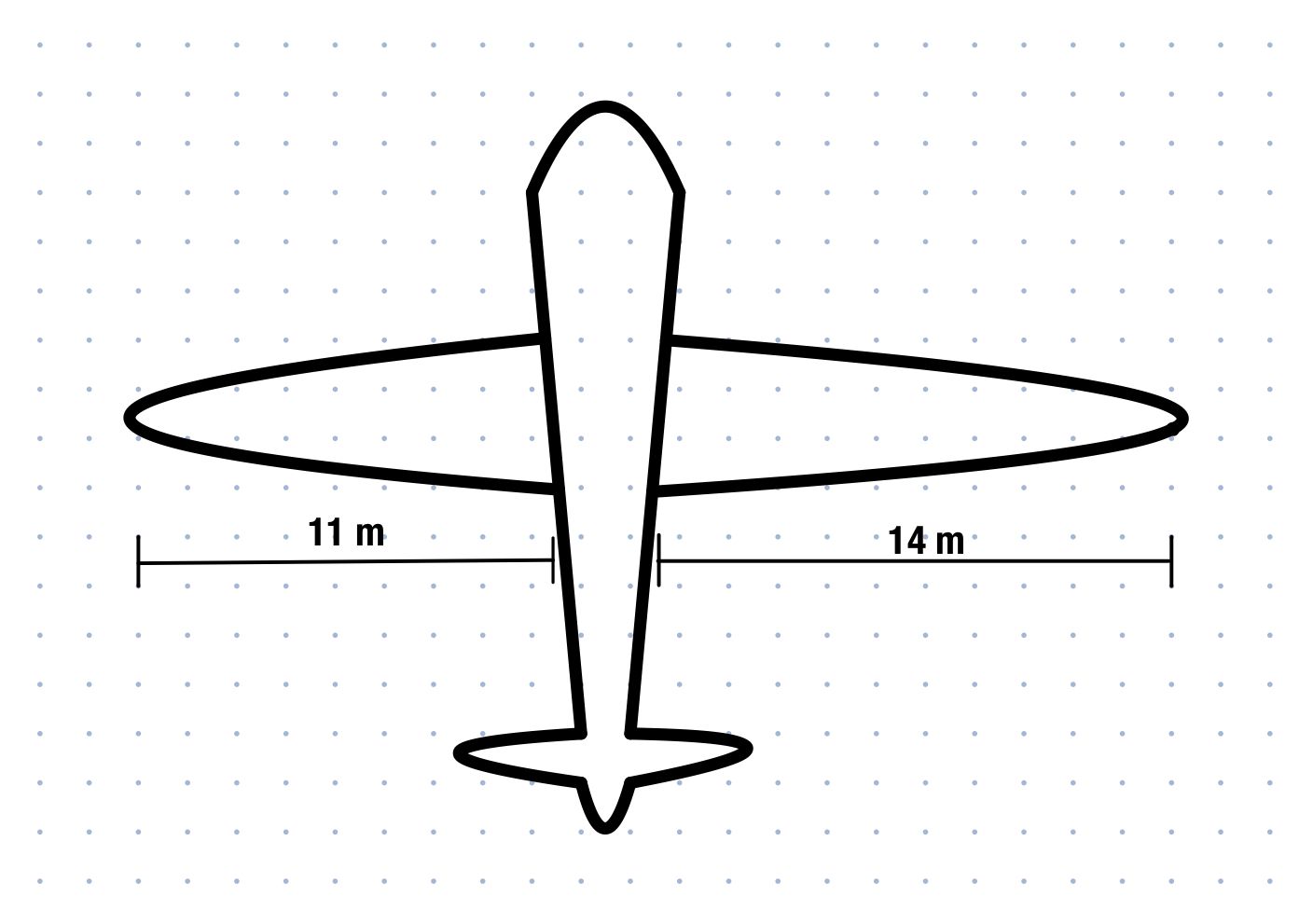
Stell dir vor, zwei Ingenieure bauen zusammen ein Flugzeug. Fr. Blöhme ist für die linke Hälfte des Flugzeugs zuständig und Hr. Doppler für die rechte. Um die Länge der Tragflächen zu berechnen, kommt nach langen und komplizierten Berechnungen folgende Schlussrechnung heraus:

3 m + 4 m ⋅ 2 = ?.

Fr. Doppler berechnet nun die Länge der linken, Hr. Blöhme die Länge der rechten Tragfläche. Hier siehst du ihre Rechnungen:

$F r . Bl \overset{o}{¨} hm e$

$3 m + 4 m \cdot 2 = ??? m$

$3 m + 8m 4 m \cdot 2 = 3 m + 8 m = \underline{\underline{11m}}$

$Hr . Do ppl er :$

$3 m + 4 m \cdot 2 = ??? m$

$7m 3 m + 4 m \cdot 2 = 7 m \cdot 2 = \underline{\underline{14m}}$

Oh nein!!!

Als die beiden Flugzeughälften zusammengebaut werden, fällt auf, dass die Tragflächen unterschiedlich lang sind! So kann das Flugzeug unmöglich fliegen!

Zuerst kann sich niemand erklären, wie das passieren konnte. Dann aber fällt dem Studenten Jakob Uhry auf, dass Hr. Doppler sich bei seinen Berechnungen nicht an die Regel "Punkt vor Strich" gehalten hat!

Wie peinlich für Hr. Doppler...

Du siehst also: die Einhaltung der Regel "Punkt vor Strich" ist in der Mathematik wirklich wichtig. Beachtest du sie nicht, bekommst du falsche Ergebnisse!

Und warum nicht Strich vor Punkt?

Auch hier ist es am besten, sich das Problem an einem Beispiel zu verdeutlichen.

Stell dir vor, Mia hat Äpfel gepflückt. Um sie zu zählen, legt sie sie in 3er-Reihen auf den Tisch.

$◯ + ◯ + ◯$

$◯ + ◯$

Um zu erfahren, wieviele Äpfel sie gepflückt hat, kann sie nun auf zwei Weisen vorgehen:

1. Durchzählen

$◯ + ◯ + ◯ + ◯ + ◯ + ◯ + ◯ + ◯ = 8 \ddot{A} p f e l$

2. Geschickt rechnen

$2 \cdot 3 \ddot{A} p f e l + 2 \ddot{A} p f e l = ??? \ddot{A} p f e l$

$6 \ddot{A} pfel 2 \cdot 3 \ddot{A} p f e l + 2 \ddot{A} p f e l = 6 \ddot{A} p f e l + 2 \ddot{A} p f e l = \underline{\underline{8 \ddot{A} pfel}}$

$◯ + ◯ 2 \cdot 3 + ◯ 2$

$◯ + ◯ + ◯$

$◯ + ◯$

Nach dem Durchzählen weiß Mia sicher, dass es 8 Äpfel sind. Und beim Geschickt rechnen ist ihr aufgefallen, dass es hier wieder eine Rechnung mit einer Punkt- und einer Strichrechnung gibt. Befolgt sie die Regel Punkt vor Strich, dann erhält sie als Ergebnis 8 Äpfel - genauso viele wie beim Durchzählen.

Was aber passiert, wenn sie diese Regel nicht befolgt und zuerst die Strichrechnung erledigt?

$2 \cdot 3 \ddot{A} p f e l + 2 \ddot{A} p f e l = ??? \ddot{A} p f e l$

$2 \cdot 5 \ddot{A} pfel 3 \ddot{A} p f e l + 2 \ddot{A} p f e l = 2 \cdot 5 \ddot{A} p f e l = \underline{\underline{10 \ddot{A} pfel}}$

Dann erhält Mia das Ergebnis 10 Äpfel. Aber das kann ja gar nicht stimmen - schließlich liegen nur 8 Äpfel auf dem Tisch!

An diesem Beispiel kann man also schön sehen, warum die Regel Punkt vor Strich Sinn macht und IMMER beachtet werden muss. Andernfalls sind die Ergebnisse falsch!