Wie du inzwischen weißt, berechnet man den Umfang und den Flächeninhalt immer im sogenannten 4-Schritt-Löseverfahren. Besteht z.B. eine Fläche aus mehreren Teilflächen, so kann die Standard-Formel (z.B. A=a⋅b) nicht mehr angewendet werden und man muss einen eigenen Term - also eine Art Formel
, die nur für diese zusammengesetzte Fläche gilt - erstellen.
(Das hast du z.B. in den Materialien AB: Umfang zusammengesetzter Flächen und AB: Die Bodenplatte bereits gemacht - vielleicht ohne es zu bemerken.)
Diesen Term nennt man Sachterm
.
Beispiel:
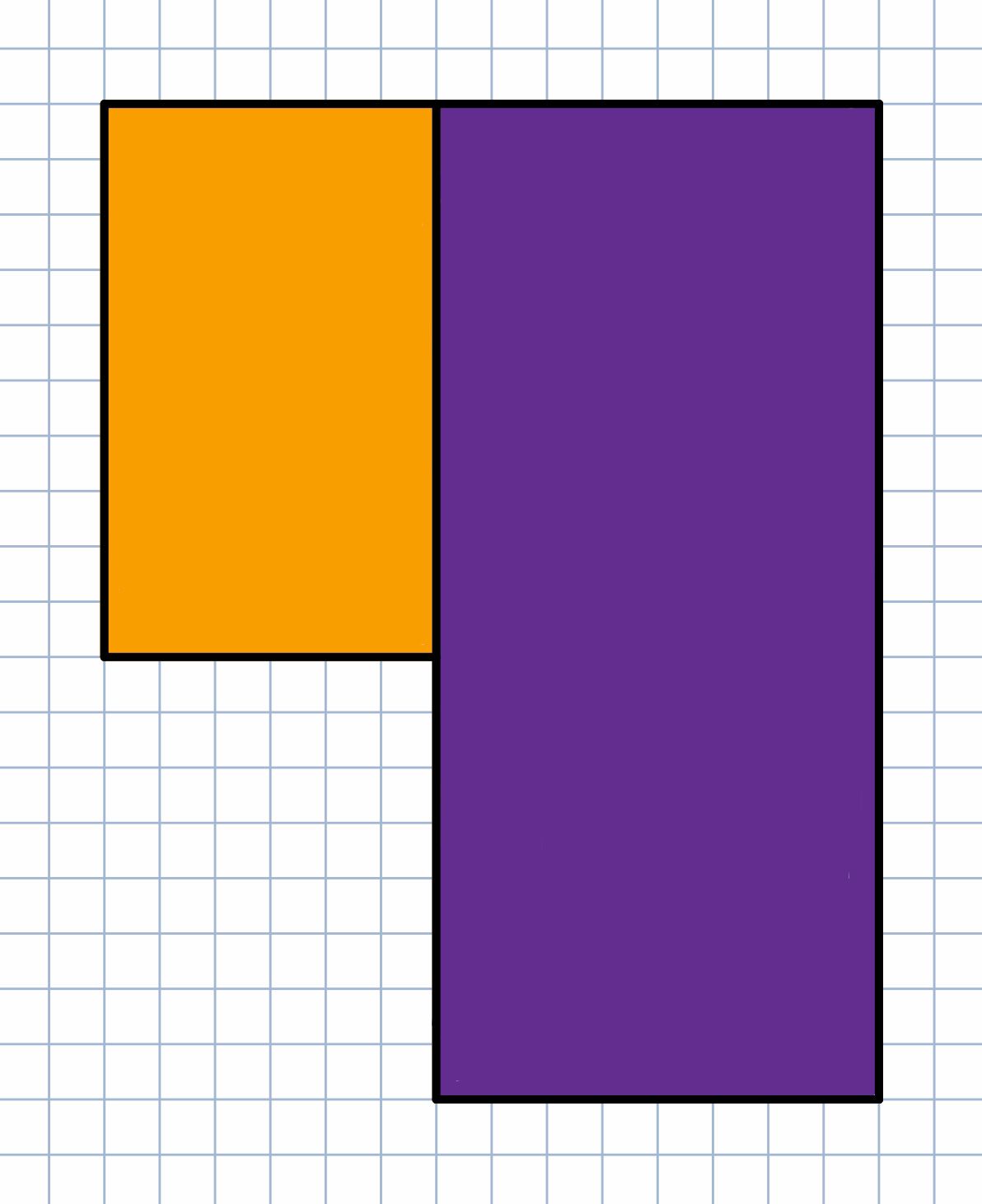
Da der Flächeninhalt einer zusammengesetzten Fläche aus der Summe der Teilflächen besteht, lautet der Sachterm in diesem Fall:
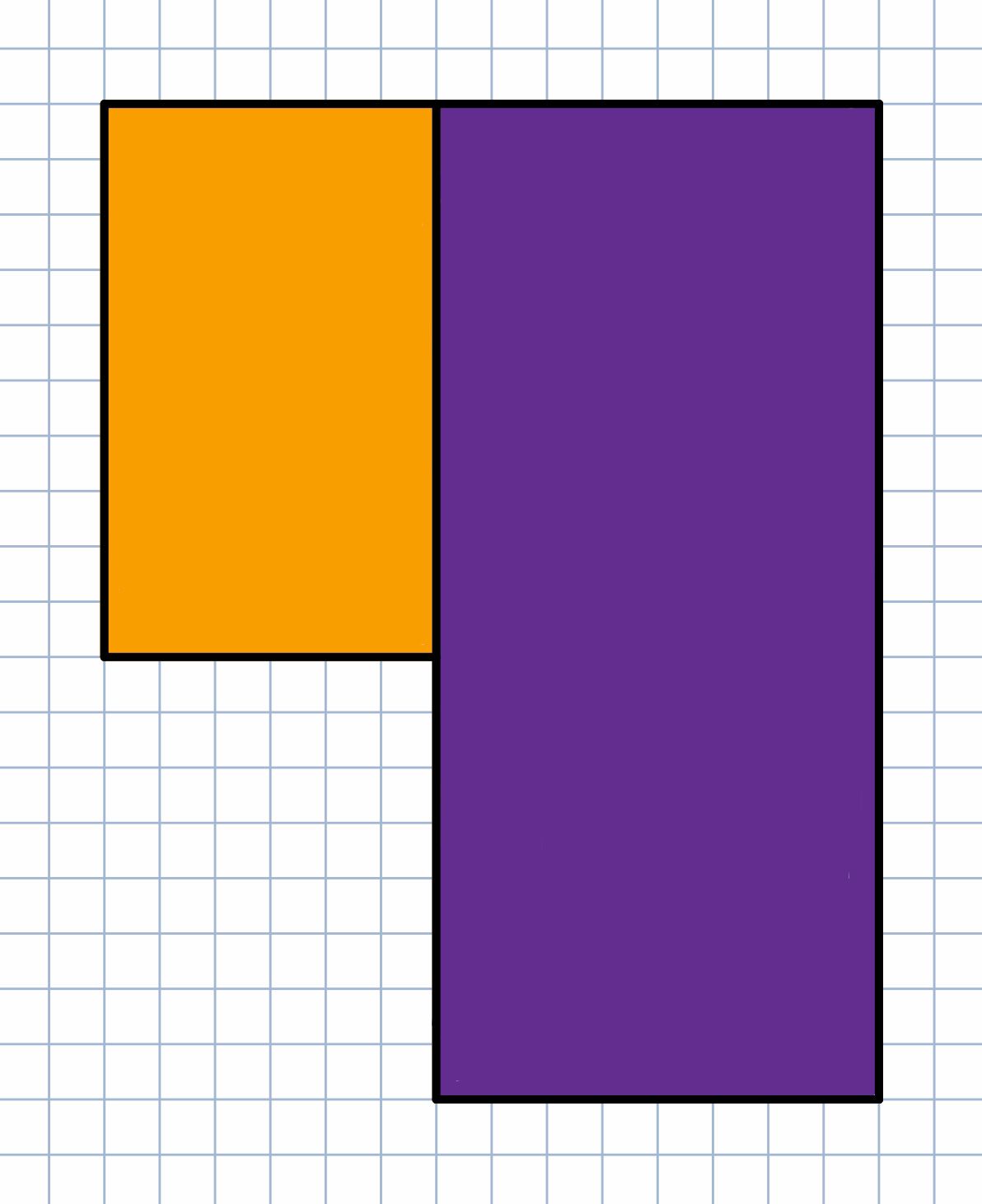
Wenn man die Teilflächen durchnummeriert, dann muss man weniger schreiben! 😜
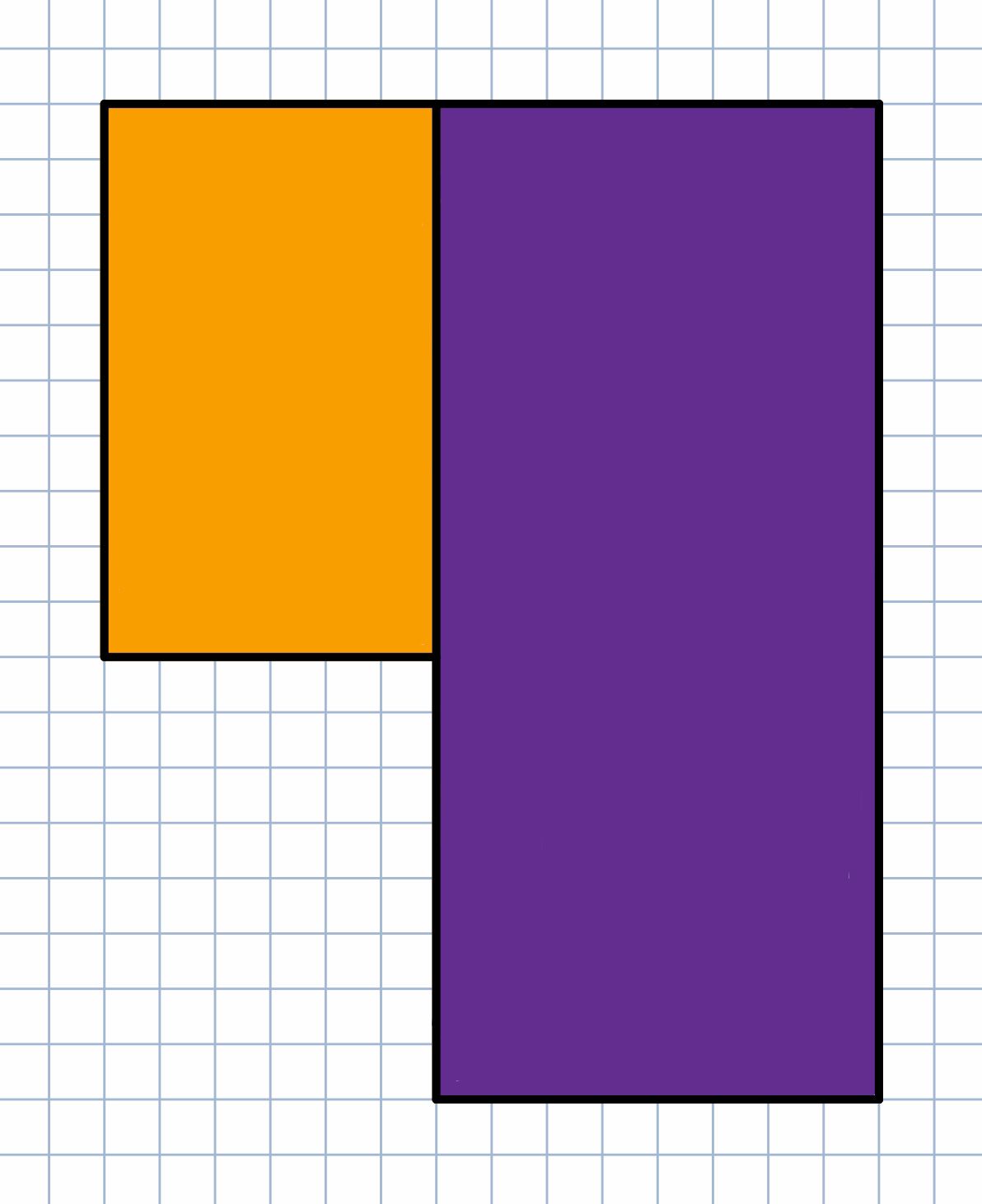
a
Der Sachterm für den Umfang lautet:
f
e
b
d
c
https://editor.mnweg.org/mnw/dokument/sachterme-aufstellen-2


