HerunterladenAls PDF Herunterladen
  • Satz des Pythagoras
  • MNWeG
  • 11.08.2023
  • Mathematik
  • Raum und Form
  • M (Mindeststandard)
  • 9
  • Einzelarbeit
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Satz des Pythagoras
Mathematik Raum und Form M 9

Das wich­tigs­te Hilfs­mit­tel der Land­ver­mes­ser im alten Ägyp­ten war eine Schnur mit zwölf Kno­ten. Mit die­ser Schnur konn­ten die Grund­stü­cke der Bau­ern nach dem Nil­hoch­was­ser neu ein­ge­mes­sen wer­den.

Diese zwölf Kno­ten hat­ten immer den glei­chen Ab­stand zu­ein­an­der und damit war es mög­lich, einen rech­ten Win­kel her­zu­stel­len.

Mit dem Satz des Py­tha­go­ras ist es mög­lich, diese zwölf Kno­ten zu er­klä­ren.

Runde deine Er­geb­nis­se immer auf eine Nach­kom­ma­stel­le.

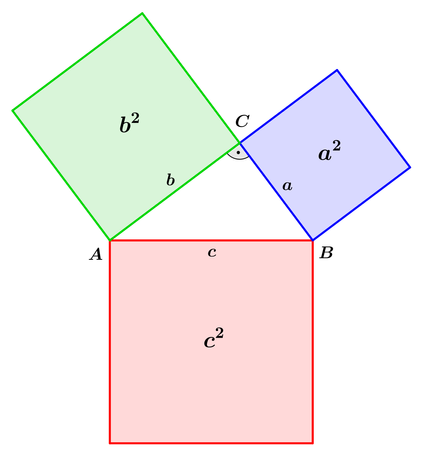
Satz des Phytha­go­ras

a2 + b2 = c2

c ist dabei immer die längs­te Seite! Sie wird Hy­po­te­nu­se ge­nannt.

Die bei­den an­de­ren Sei­ten sind die

Ka­the­ten.

Der Win­kel zwi­schen den Ka­the­ten ist immer ein 90° Win­kel!

1
Hier nun eine Auf­ga­be zur 12-​Knoten-Schnur.
Die Ka­the­ten a = 3 m und b = 4 m bil­den einen rech­ten Win­kel.
Be­rech­ne die Länge der Hy­po­te­nu­se c.
Be­rech­ne an­schlie­ßend den Um­fang des
Drei­eckes und ver­glei­che die­sen mit der
12-​Knoten-Schnur.
2
In einem recht­wink­li­gen Drei­eck sind die Ka­the­ten a = 9 dm und b = 7,8 dm lang.
Be­rech­ne die Länge der Hy­po­thenu­se c.
3
In einem recht­wink­li­gen Drei­eck be­trägt die Länge der Ka­the­te a = 9,8 cm und die der Hy­po­thenu­se c = 17,5 cm.
Be­rech­ne die Länge der feh­len­den Ka­the­te b.
4
Hier siehst du ein gleich­sei­ti­ges Drei­eck mit der Sei­ten­län­ge 5 cm.
Be­rech­ne die Höhe des Drei­eckes.
5
Be­rech­ne die Stre­cke des Tra­pe­zes.
Bereitgestellt von: MNWeG Stand: 11.08.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/satz-des-pythagoras-12
Seite: 1/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/satz-des-pythagoras-12
AB
Satz des Pythagoras
Mathematik Raum und Form M 9
6
Wel­che recht­wink­li­gen Drei­ecke könn­ten ge­zeich­net wer­den? Be­wei­se dies rech­ne­risch!
Lö­sungs­satz nicht ver­ges­sen!
  • a = 12 cm; b = 16 cm; c = 20 cm
  • a = 4 cm; b = 5 cm; c = 6 cm
  • a = 6 m; b = 8 m; c = 10 m
  • a = 10,5 dm; b = 5,3 dm; c = 12,4 dm
7
Be­rech­ne die Dia­go­na­le einer Raute mit der Sei­ten­län­ge 6 cm. Die Dia­go­na­le hat eine Länge von 9 cm.
Zeich­ne vor­her un­be­dingt in die Skiz­ze ein, wel­che An­ga­ben du schon hast.
8
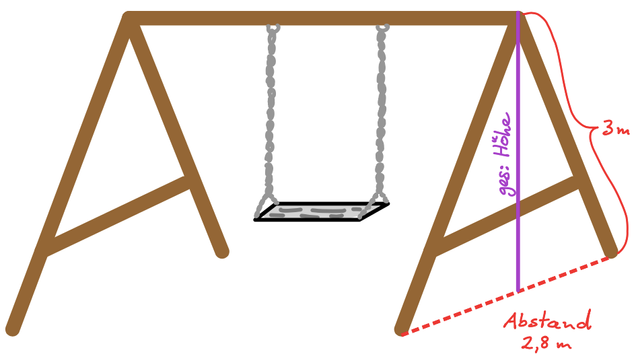
Hier siehst du die Skiz­ze einer Schau­kel.
Be­rech­ne die Höhe der Schau­kel.
Zeich­ne vor­her un­be­dingt in die Skiz­ze ein,
wel­che An­ga­ben du schon hast.
Also was ist a, b, c und was ist ge­sucht?
9
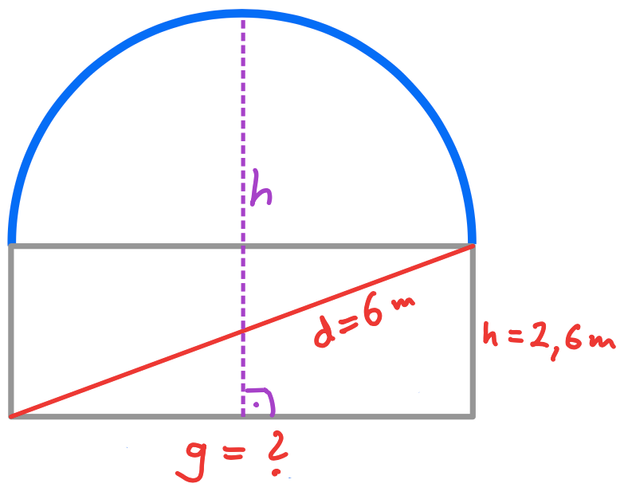
Hier siehst du die Skiz­ze eines Pla­ne­ta­ri­ums.
Be­rech­ne die Ge­samt­hö­he des Pla­ne­ta­ri­ums.
Bereitgestellt von: MNWeG Stand: 11.08.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/satz-des-pythagoras-12
Seite: 2/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/satz-des-pythagoras-12
AB
Satz des Pythagoras
Mathematik Raum und Form M 9
10
Eine Lei­ter ist 4 m lang und soll in 3,5 m Höhe an die Wand ge­lehnt wer­den.
In wel­chem Ab­stand von der Wand steht dann das un­te­re Ende der Lei­ter?
Fer­ti­ge zu­nächst eine Skiz­ze an!
11
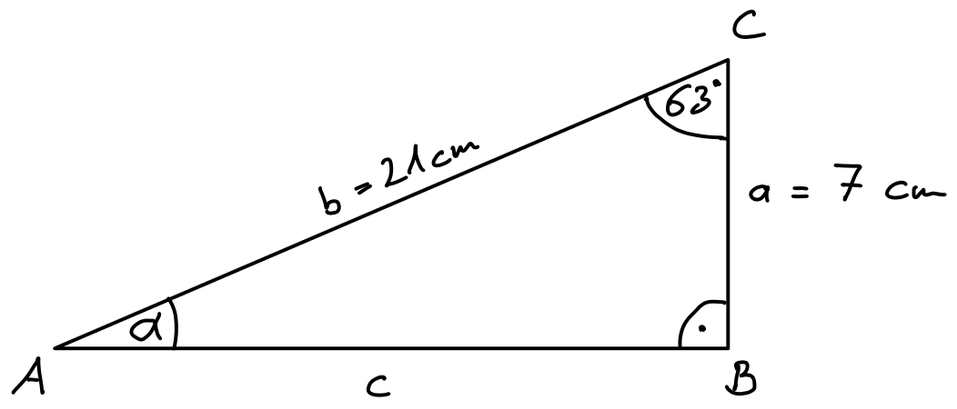
Be­rech­ne die feh­len­de Sei­ten­län­ge und den Win­kel α.
Bereitgestellt von: MNWeG Stand: 11.08.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/satz-des-pythagoras-12
Seite: 3/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/satz-des-pythagoras-12
x