Jedes Mal, wenn du online eingekauft hast, hat die Plattform für deinen Einkauf einen Term aufgestellt, um die Gesamtsumme zu errechnen.

Hast du z.B. 5 Fasermaler und 3 Geodreiecke in den Einkaufswagen getan, dann sieht dein Einkaufswagen wie folgt aus:

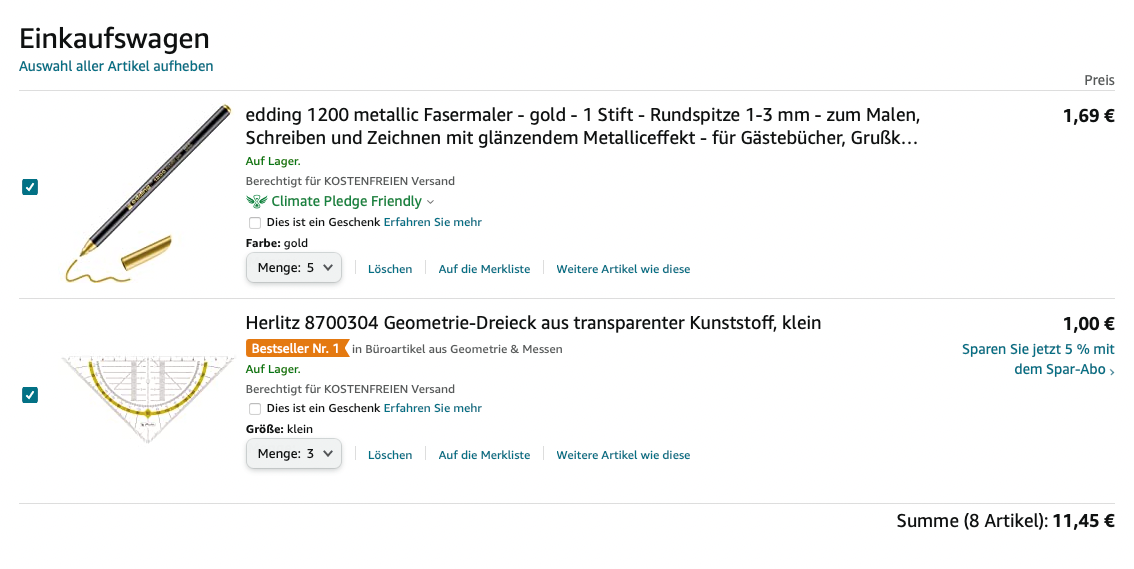
Der Term, den die Plattform automatisch im Hintergrund aufstellt, sieht dann in etwa so aus:









Dabei steht die Variable $f$ für Fasermaler und $g$ für Geodreieck.

Da insgesamt $5$ Mal der Fasermaler ($f$) gekauft werden soll, kann man die fünf Variablen auch zusammenfassen. Gleiches gilt auch für die Geodreiecke ($g$):









Da in der Datenbank hinterlegt ist, dass $1\cdot f$ genau $1,69€$ und $1\cdot g$ genau $1,00€$ kostet, kann nun die Gesamtsumme berechnet werden:

Dieser Term soll vereinfacht werden.

1.: Als erstes sortieren wir den Term einmal. Dabei gruppieren wir jede Variable:

2.: Nun können die Gruppen zusammengefasst oder vereinfacht werden:

Der Term oben wird also wie folgt geschrieben: