Terme

1

Ordne und fasse die Terme zusammen.

x + 8x - 3x + x
2a + a + 5 - a + 12
5k - 15 + 11 - k + 4 - 3k
2a + 4b - 4a + b - 3b
0,5y + 0,3x + 1,2x - 1,5y - 2x
- 3x + 8 - 2y - 2 + x - y - 7

Achtung

Rechenzeichen und Vorzeichen beachten!

2

Löse die Klammern auf und fasse zusammen.

3 · (x + 7)
7 · (2a + 3b)
4 · (a - 2b) - 2a + 3b
- 2 · (x - 3b) - 3b
5 · (2a - 3b) - 2 · (a + b)
8 · (a - b) - 3 · (a + b)

3

Ersetze x durch die angegebene Zahl und berechne das Ergebnis.

x = 2 $\to$ x + 7 + 2x
x = 5 $\to$ 2x + 3 - 3x
x = 1,5 $\to$ 4x - 5 + 2x - x
x = 0,5 $\to$ - 5 + 2x + 3x + 2 - x

4

Ersetze die Variablen durch die angegebenen Zahlen und berechne das Ergebnis.
a = 3; b = 4; x = 2; y = 5
Z.B.: 3a - 2b + 12 - b - 6 = 3 · 3 - 2 · 4 + 12 - 4 - 6 = 9 +12 - 8 - 4 - 6 + 21 - 18 = 3

- 14 + 4b - a + b + 3a + 5
- 2x - 3y + 8 - x + 2 + 2y
- 5x + 8 + 3 · (a - b)
- 3 · (5x - 4) + 2 · (x - y)

Merkwissen Terme

- Terme bestehen aus Zahlen und/oder Variablen.

Z.B. ist 5 oder 294 ein Term, aber auch 2x oder 3y + 4z - a.

Dabei ist 2x die Kurzschreibweise für 2 · x.

- Terme können vereinfacht werden.

Z.B. 2x + y + 3x + 2y = 5x + 3y

- Buchstaben wie a, x, y oder auch andere Symbole und Zeichen werden als Variablen

bezeichnet.

- Wenn für die Variablen Zahlen eingesetzt werden, können Terme auch gelöst werden.

Z.B. wenn wir bei 5x für x eine 2 einsetzen, dann ergibt sich 5 · 2 = 10.

5

Schreibe zu den Aussagen einen passenden Term.

Anton erhält 15 € Taschengeld für x Monate.
Kannst du für die Taschengeldaufgabe a) auch einen Term für y Jahre aufstellen?
In einem Restaurant gibt es zwei verschiedene Burger, die sehr häufig verlangt werden. Einer kostet 5,95 €, der andere 7,95 €.
Lernpartner*innen organisieren einen Sponsorenlauf.
Für jede Runde im Stadion zahlt der Sponsor 0,50 €.
Pro Kilometer zahlt er zusätzlich 1 €. Stelle einen Term auf.
Peter hat einen Telefontarif, bei dem er pro Monat 9,99 € bezahlt.
Pro Einheit muss er zusätzlich noch 0,9 ct bezahlen.
Stelle einen passenden Term für einen Monat und mehrere Monate auf.

6

Verbinde die passenden Terme.

2 (x - 4b)

2x + 6b

8b + 2x

Tipp

Wenn du die Terme zusammenfasst oder

die Klammern auflöst, geht es einfacher.

2 (x - 2b) + 2b

12 - 8b - 4 + x - 3x

2b + 4x

8 - 8b - 2x

x + 4b + 2x - 2b + 3x

Merkwissen Terme und Gleichungen

- Beim Auflösen von Klammern unbedingt die Rechenzeichen und Vorzeichen beachten.

- Es gilt: - · - = + und + · + = + und + · - = - und - · + = -

- Der Term vor der Klammer wird mit jedem Term in der Klammer nacheinander

multipliziert, z.B. - 2 (x + 4) = - 2 · x - 2 · (+ 4) = - 2x - 8

- Achtung: Der Term, mit dem multipliziert wird, kann auch hinter der Klammer stehen,

z.B. (x + 4) · (- 2). Das Ergebnis ist das Gleiche wie oben.

- Negative Rechenzeichen, das heißt - vor der Klammer, drehen die Vorzeichen in der

Klammer beim Auflösen um. Z.B. - (4 - x) = - 4 + x

Beachte: vor der 4 in der Klammer steht gedanklich ein +.

Gleichungen

7

Löse die Gleichungen und mache anschließend die Probe.

6a - 15 = 15
25 + 4x = 13 + 2x
2,5y - 5 = y + 1
- 4a - 3 = - 2a + 5

Beachte

Löse die Aufgaben immer so, dass die Gleichheitszeichen genau untereinander stehen.

8

Löse die Gleichungen. Fasse vorher zusammen.

- 3x + 15 + x - 3 = 2x + 8 - 7x + x
2,5a - 13 - a = 15 - a + 3 + 2a - 8
4b + 10 - b - 5 = 2b - 12 + 3b + 7
- 2x + 5 - 0,5x - 21 = 3x - 5x - 4

9

Multipliziere zuerst die Klammern aus und löse dann die Gleichungen.

10x + 7 = - 3 · (-2x + 3)
5 · (5 + 2y) - 4y = 3y - 7 - y
2 · (- x + 7) - 9 = 2x - 3 · (2x - 4)
0,5 · (4x - 16) = 8x - 8 - 5x + 6

10

Stelle je eine Gleichung auf und löse diese.

Multipliziert man eine Zahl mit 3, so erhält man 27 subtrahiert um die Zahl 9.
Wenn ich eine Zahl mit dem Vierfachen multipliziere, dann erhalte ich das
Doppelte der Zahl addiert mit 7.
Das Doppelte der Zahl subtrahiert um 11 ist das Gleiche wie 14 dividiert durch 2.
Das Vierfache einer Zahl ist um 21 größer als das Dreifache der Zahl.
Ein Parallelogramm ist 2 cm breiter wie die andere Seite. Der Umfang beträgt 52 cm.
Gebe die Seiten a und b an.
Lisa und Fritz sind zusammen 25 Jahre alt. Lisa ist 3 Jahre älter als Fritz.
Berechne das Alter der beiden.

APP mit Gleichungen incl. Lösungen

Merkwissen Gleichungen

- Eine Gleichung kannst du dir wie eine Waage vorstellen.

- Wenn du auf beiden Seiten das Gleiche rechnest, dann bleibt die Waage im Gleichgewicht.

- Steht ein Bruch vor einer Variablen, also z.B. $\frac{1}{3}$ x, dann musst du mit dem Kehrwert des Bruches multiplizieren, also mit $\frac{3}{1}$ . Das Ergebnis wäre dann 1x.

Diese 1 vor dem x wird jedoch nicht geschrieben.

- Steht eine negative Zahl vor einer Variablen, also z.B. - 3x, dann musst du durch die

negative Zahl dividieren, also durch - 3. Da $\frac{- 3}{- 3}$ = 1 ist, wäre wieder 1x die Lösung,

wobei die 1 erneut nicht geschrieben wird.

- Mit einer Probe, also dem Einsetzen des Ergebnisses in die Ausgangsgleichung,

kannst du deine Lösung immer überprüfen.

A2/B - Aufgaben

Löse mit dem Taschenrechner

11

Die Enkel Lisa, Fritz und Klaus sind zusammen so alt wie ihr Opa Franz. Opa Franz ist 82 Jahre alt. Lisa ist die Jüngste und 6 Jahre jünger als Fritz. Klaus ist doppelt so alt wie Fritz.
Wie alt ist Lisa?

12

Der Umfang eines Rechteckes ist genau so groß wie der Umfang eines Quadrates.
Das Quadrat hat einen Umfang von 36 cm. Die Seitenlänge b des Rechteckes ist
doppelt so lang wie a.
Wie lang sind die Seiten a und b des Rechteckes?

13

Das Dreieck und das Rechteck haben den gleichen Umfang. Berechne die Seitenlänge x.

Privat: A. Schöler

14

Familie Müller möchte Dekodrachen bauen. Der Rand des Drachens soll mit Holzleistchen stabilisiert werden.
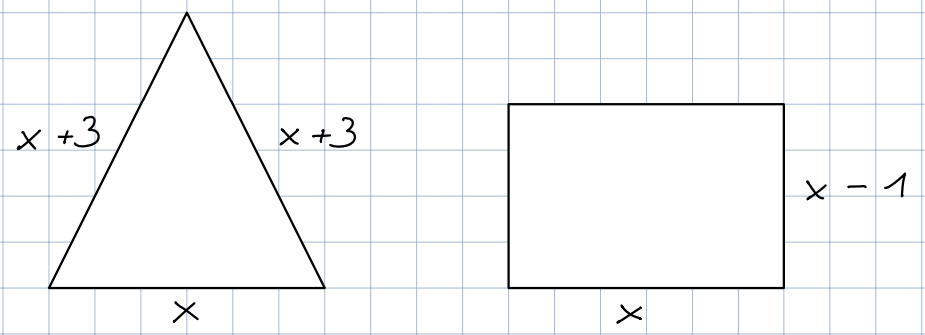
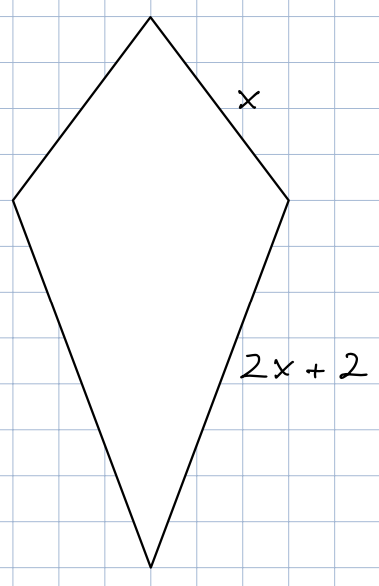
Wie lang ist jeweils das kurze und das lange Leistchen,
wenn die gesamte Leiste eine Länge von 124 cm hat?

Terme

Glei­chun­gen

Gleichungen