Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Info
Umfang und Flächeninhalt
Mathematik M 9
Hier findest du Videos zu allen geometrischen Formen, von denen du die Flächen berechnen
können solltest.
können solltest.
- Tipp: Video anschauen und gleich die Formeln rechts daneben aufschreiben.
- Anschließend die Beispiele berechnen. Aufgaben auf einem karierten Blatt lösen.
Gegeben: a = 5 cm
u =
A =
Gegeben: a = 4 cm, b = 2,5 cm
u =
A =
Gegeben: a = 4 cm, b = 3 cm, ha = 2,5 cm
u =
A =
Gegeben: a = 4 cm, b = 3 cm, c = 2 cm, d = 3 cm, ha = 2,5 cm
u =
A =
Gegeben: a = 4 cm, b = 3 cm, c = 4 cm, ha = 2,8 cm
u =
A =
Gegeben: r = 3 cm, d = 6 cm
u =
A =
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-7
https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-7
Info
Umfang und Flächeninhalt
Mathematik M 9
Alle Formeln im Überblick
Name | Umfang = u | Flächeninhalt = A | |
|---|---|---|---|
Quadrat |
|
| |
Rechteck |
|
| |
Parallelo-gramm g = a |
|
| |
Trapez |
| A = 2a+c · h | |
Dreieck |
| A = 2a⋅ha oder 2g⋅hg | |
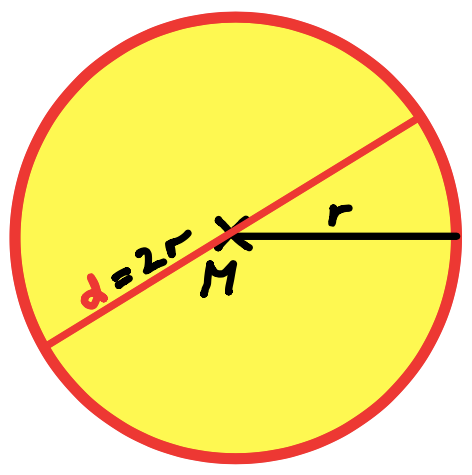
Kreis |
| A = π · r2 |
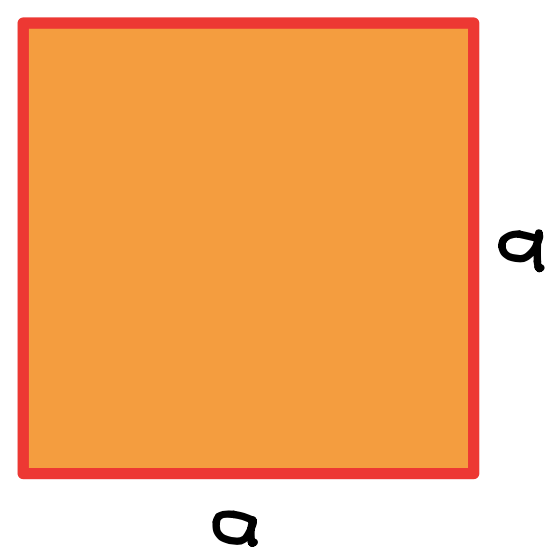
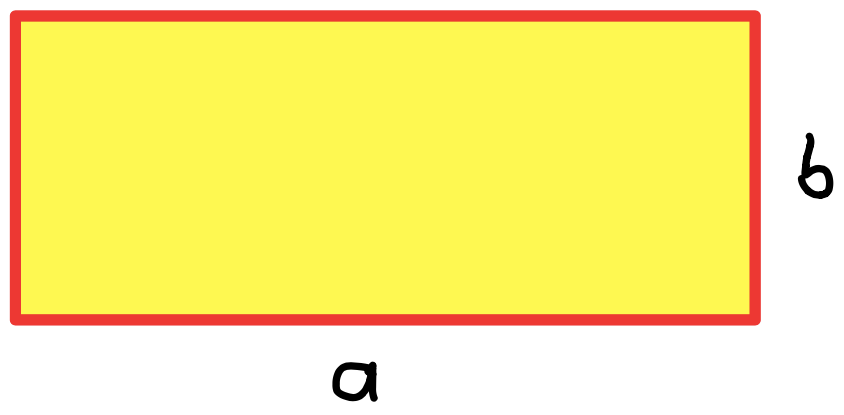


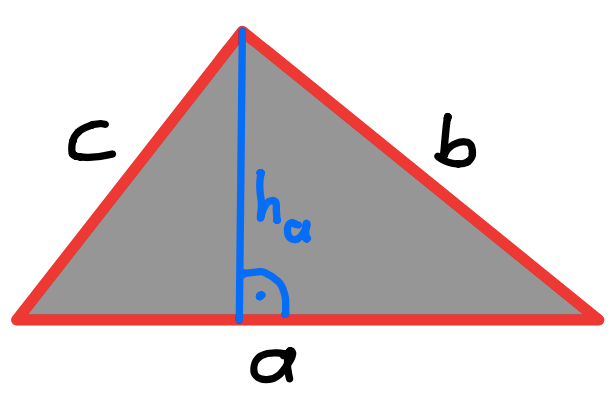
jede Seite, also a, b oder c, kann unten sein
AUSFÜLLEN | AUFHÄNGEN | LERNEN
Merke
Die Summe aller Innenwinkel im Dreieck beträgt immer 180°.
Gleichseitiges Dreieck
- alle Seiten gleich lang
- alle Winkel 60°
Merke
Die Summe aller Innenwinkel im Viereck beträgt immer 360°.
Gleichschenkliges Dreieck
zwei Seiten gleich lang
zwei Winkel gleich groß
Spitzwinkliges Dreieck
- alle drei Winkel kleiner 90°
Rechtwinkliges Dreieck
- ein rechter Winkel (90°)
- Satz des Pythagoras (Teil 3)
a2 + b2 = c2
Stumpfwinkliges Dreieck
- genau ein Winkel größer 90°
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-7
https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-7


