HerunterladenAls PDF Herunterladen
  • Umfang und Flächeninhalt
  • MNWeG
  • 11.08.2023
  • Mathematik
  • M (Mindeststandard)
  • 9
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Umfang und Flächeninhalt
Mathematik M 9

Teil A1 - Auf­ga­ben

OHNE Ta­schen­rech­ner

Wich­tig

Los geht es immer mit der For­mel.

In die For­mel wer­den die ge­ge­be­nen An­ga­ben ein­ge­setzt und dann erst wird die Auf­ga­be ge­löst.

1
Be­rech­ne den Um­fang und den Flä­chen­in­halt eines Qua­dra­tes mit a = 3 cm.
2
Be­rech­ne den Um­fang und den Flä­chen­in­halt eines Recht­eckes mit a = 3 cm und b = 5 cm.
3
Du hast ein Recht­eck mit einem Flä­chen­in­halt von 28 dm2.
Nenne mög­li­che Län­gen der Seite a und b.
4
Ein Qua­drat hat einen Flä­chen­in­halt von 225 mm2. Wie lang ist eine Seite? Wie groß ist der Um­fang?
5
Be­rech­ne den Um­fang und den Flä­chen­in­halt eines
Par­al­lo­gramms mit a = 3 cm, b = 5 cm und h = 4 cm.
6
Be­rech­ne den Um­fang und den Flä­chen­in­halt eines
Tra­pe­zes mit a = 5 cm, b = 3 cm, c = 4 cm, d = 3 cm, h = 3,5 cm.
7
Be­rech­ne den Um­fang und den Flä­chen­in­halt eines Drei­eckes mit a = 5 cm, b = 3 cm, c = 4 cm, ha = 4 cm.
8
Ein gleich­sei­ti­ges Drei­eck hat einen Um­fang von
18 cm und die Höhe ha = 5,2 cm.
Wie lang ist die Sei­ten­län­ge a des Drei­eckes?
Wie groß ist der Flä­chen­in­halt des Drei­eckes?
9
Be­rech­ne den Um­fang und den Flä­chen­in­halt eines Krei­ses mit r = 4 dm.
10
Ein Kreis hat einen Um­fang von 18,84 cm.
Wie groß ist der Ra­di­us und der Flä­chen­in­halt?
Bereitgestellt von: MNWeG Stand: 10.01.2024 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-8
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-8
AB
Umfang und Flächeninhalt
Mathematik M 9
11
Wie ver­än­dert sich der Flä­chen­in­halt eines Par­al­le­lo­gram­mes, bei fol­gen­den Ver­än­de­run­gen?
  • Die Länge der Grund­sei­te wird ver­dop­pelt.
  • Die Höhe wird hal­biert.
  • Die Länge der Grund­sei­te und Höhe wird ver­dop­pelt.
12
Ein Par­al­le­lo­gramm hat eine Brei­te von 8,5 cm und einen Flä­chen­in­halt von 136 cm2.
Wel­che Höhe hat das Par­al­le­lo­gramm?

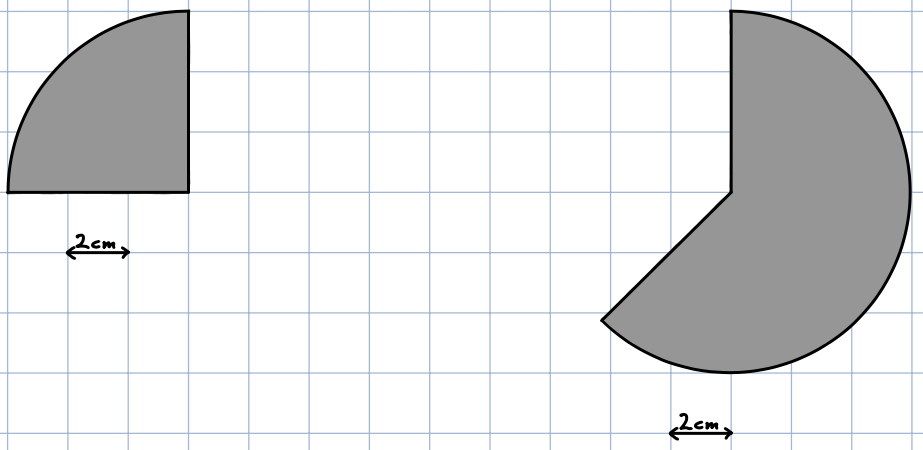
A

13
Be­rech­ne den Flä­chen­in­halt und den Um­fang der grau mar­kier­ten Flä­che.

B

14
Der Um­fang eines Krei­ses be­trägt 163,25 dm.
Wie groß ist der Flä­chen­in­halt?
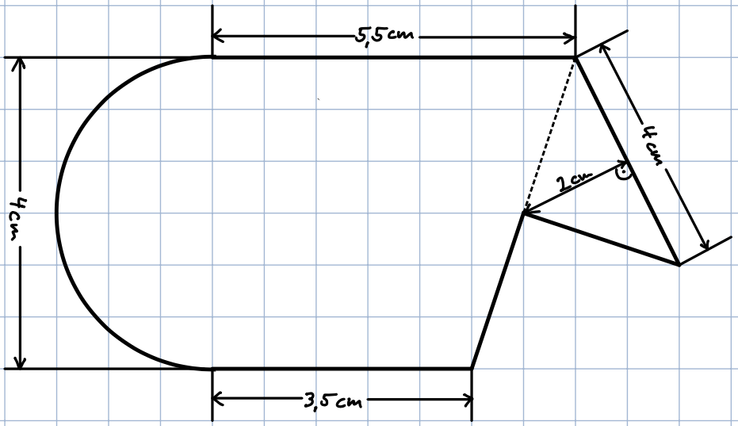
15
Wie groß ist der Flä­chen­in­halt der
zu­sam­men­ge­setz­ten Flä­che?
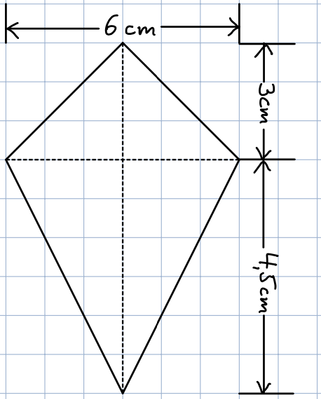
16
Be­rech­ne den Flä­chen­in­halt des Dra­chens.
Erst genau an­schau­en. Ist ei­gent­lich ganz ein­fach.
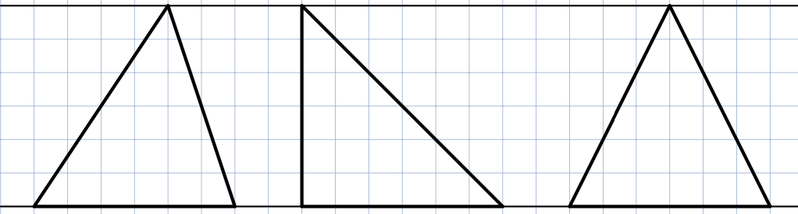
17
Schaue dir die drei Drei­ecke an. Was kannst du über deren Flä­chen­in­halt sagen?
Be­grün­de deine Aus­sa­ge.
Bereitgestellt von: MNWeG Stand: 10.01.2024 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-8
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/umfang-und-flaecheninhalt-8
x