Die Grundlagen für dieses Materialpaket wurden im Paket Messen M 5 gelegt. Alles, was du dort gelernt hast, brauchst du auch hier!
Deshalb steht am Anfang dieses Pakets eine kurze Wiederholung.
Wiederholung 1: Umfang eines Rechtecks
Im Mindeststandard haben wir uns den Umfang eines Rechtecks als Zaun einer Pferdeweide vorgestellt.
Hat die Weide also die Seitenlängen
und , dann hat die Weide einen Umfang von , denn laut der Definition...
Der Umfang eines Rechtecks errechnet sich aus der Summe aller Seiten.
... müssen alle Seiten des Rechtecks miteinander addiert werden. Als Rechnung sieht das so aus:
Wiederholung 2: Flächeninhalt eines Rechtecks
Im Mindeststandard haben wir uns den Flächeninhalt eines Rechtecks als Wiese einer Pferdeweide vorgestellt.
Durch das Parkettieren der Pferdekoppel mit Quadraten der Größe haben wir festgestellt, dass solcher Einheitsquadrate hineinpassen. Die Weide hat also einen Flächeninhalt von Einheitsquadraten.
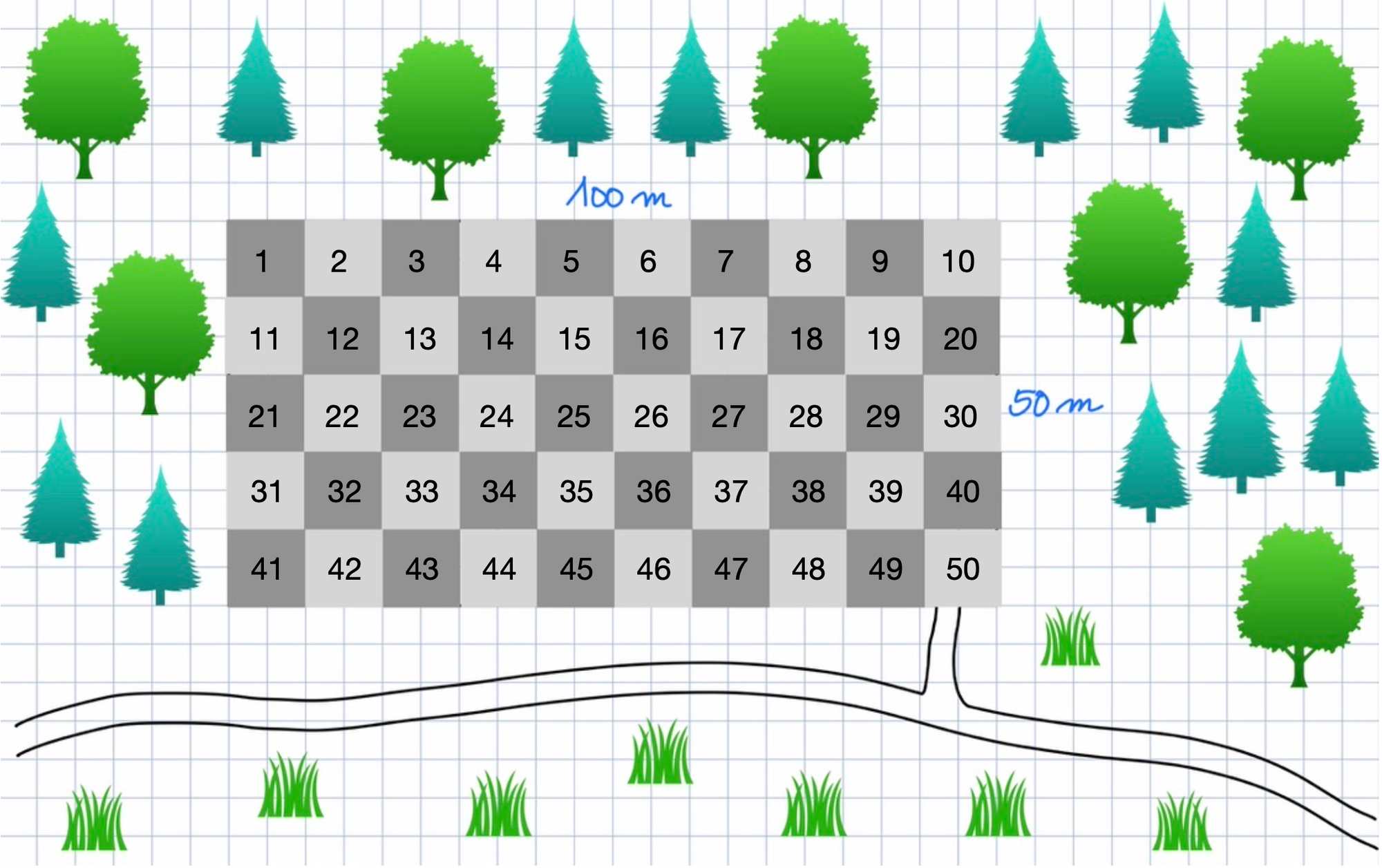
Anstatt jedes Einheitsquadrat in der Pferdekoppel durchzuzählen, kann man natürlich auch einfach wie folgt vorgehen:
Da die Pferdekoppel Einheitsquadrate lang und Einheitsquadrate breit ist, kann man einfach rechnen:
