Zufallsexperimente

AB
Zufallsexperimente
Mathematik Wahrscheinlichkeit M 9
1
Gebe die Wahr­schein­lich­keit für fol­gen­de Aus­sa­gen als (ge­kürz­ten) Bruch an.
Wie hoch ist die Wahr­schein­lich­keit, dass …

a) bei einem Münz­wurf die Zahl fällt?

b) beim Wür­feln eine 6 ge­wür­felt wird?

c) beim Wür­feln eine ge­ra­de Zahl ge­wür­felt wird?

d) mit zwei Wür­feln eine 6 ge­wür­felt wird?

e) aus 32 gut ge­misch­ten Kar­ten ein Ass ge­zo­gen wird?

f) mit zwei Wür­feln gleich­zei­tig eine 4 ge­wür­felt wird?

g) aus 32 gut ge­misch­ten Kar­ten eine rote Karte ge­zo­gen wird?
2
In einer Grup­pe mit 30 Män­nern und Frau­en sind 12 Mit­glie­der männ­lich.
Ins­ge­samt spie­len 18 Mit­glie­der Bas­ket­ball, fünf der Män­ner spie­len kein Bas­ket­ball.

Ver­voll­stän­di­ge die Ta­bel­le.












Gebe nun die Wahr­schein­lich­keit dafür an (als ge­kürz­ter Bruch oder in %), dass ...
  • unter allen Spie­ler*innen je­mand kein Bas­ket­ball spielt.

  • unter allen Spie­ler*innen eine weib­li­che Bas­ket­ball­spie­le­rin ge­zo­gen wird.

  • unter den männ­li­chen Mit­glie­dern ein Bas­ket­bal­ler ge­zo­gen wird.

Basketball

kein Basketball

männlich

5

12

weiblich

18

30

Bereitgestellt von: MNWeG Stand: 27.10.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/zufallsexperimente-6
Seite: 1/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/zufallsexperimente-6
AB
Zufallsexperimente
Mathematik Wahrscheinlichkeit M 9
3
In einer Grup­pe wur­den Ju­gend­li­che nach ihrem Lieb­lings­es­sen und ihrem Hobby ge­fragt.
Das Er­geb­nis wurde in einer Ta­bel­le dar­ge­stellt.
Gebe die Wahr­schein­lich­keit als ge­kürz­ter Bruch oder in % an.
  • Lisa möch­te wis­sen, wie hoch die Wahr­schein­lich­keit ist, bei zu­fäl­li­gem Aus­wäh­len eine(n) Ju­gend­li­che*n mit dem Hobby „Schwim­men“ zu wäh­len.

  • Paul würde gerne er­fah­ren, wie hoch bei so einem Zu­falls­ver­such die Wahr­schein­lich­keit wäre, eine(n) Ju­gend­li­che*n mit einem Alter unter 16 Jah­ren aus­zu­wäh­len.

  • Emily fragt sich, wie hoch die Wahr­schein­lich­keit wäre, eine(n) Ju­gend­li­che*n mit dem
    Lieb­lings­es­sen Sushi aus­zu­wäh­len.

  • Stel­le die Al­ters­ver­tei­lung für die Grup­pe gra­phisch dar. Zeich­ne ein Kreis­dia­gramm mit den je­wei­li­gen pro­zen­tu­a­len An­tei­len der 14-, 15- und 16-​jährigen.
    Hin­weis: Be­schrif­tung nicht ver­ges­sen!

Name

Geschlecht

Alter

Lieblingsessen

Hobby

Olaf

m

14

Spaghetti

Zeichnen

Lisa

w

16

Hamburger

Schwimmen

Yasmin

w

14

Pizza

Fußball

Emmeth

m

15

Hamburger

Fußball

Paul

m

16

Pommes

Trompete

Lara

w

16

Spaghetti

Tanzen

Emily

w

14

Döner

Zeichnen

Mario

m

15

Sushi

Fußball

Jana

w

14

Pizza

Schwimmen

Thomas

m

15

Pommes

Lesen

Bereitgestellt von: MNWeG Stand: 27.10.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/zufallsexperimente-6
Seite: 2/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/zufallsexperimente-6
AB
Zufallsexperimente
Mathematik Wahrscheinlichkeit M 9
4
In einem Los­topf be­fin­den sich fünf Ku­geln in fünf ver­schie­de­nen Far­ben (grün, rot, blau, gelb und weiß). Gebe die Wahr­schein­lich­keit als ge­kürz­ten Bruch oder in % an.
  • Wie hoch ist die Wahr­schein­lich­keit, dass du zu­erst die rote Kugel ziehst?

  • Wie hoch ist die Wahr­schein­lich­keit, dass du, nach­dem du die rote Kugel ge­zo­gen hast,
    als nächs­tes die blaue Kugel ziehst?

  • Schrei­be alle mög­li­chen Zug­rei­hen­fol­gen auf, wenn die rote und die blaue Kugel
    be­reits ge­zo­gen wur­den.
    Kannst du davor schon sagen, wie viele Kom­bi­na­ti­ons­mög­lich­kei­ten es gibt?
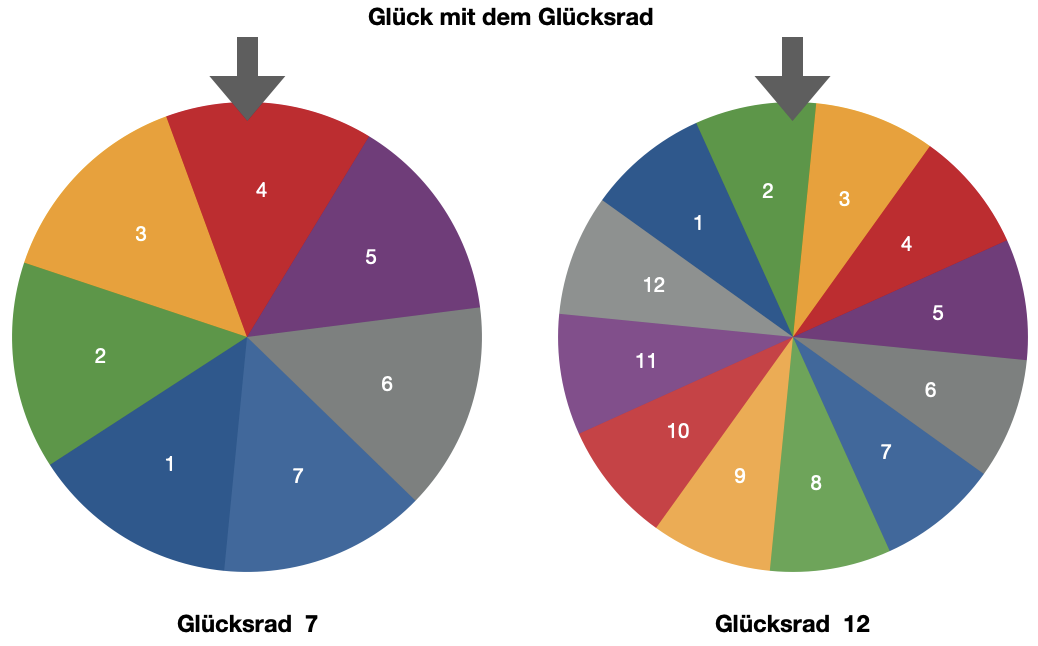
5
Hier siehst du zwei ver­schie­de­ne Glücks­rä­der. Du hat nun die Mög­lich­keit, dich für eines
der bei­den zu ent­schei­den.
  • Wel­ches Glücks­rad wür­dest du wäh­len, um mit einer un­ge­ra­den Zahl zu ge­win­nen?
    Be­grün­de deine Ent­schei­dung rech­ne­risch.

  • Wel­ches Glücks­rad wür­dest du wäh­len, um eine durch fünf teil­ba­re Zahl zu er­spie­len?
    Be­grün­de deine Ent­schei­dung rech­ne­risch.

  • Wel­ches Glücks­rad wählst du, um die Zahl 3 zu er­rei­chen?
    Be­grün­de deine Ent­schei­dung rech­ne­risch.

  • Wie hoch ist die je­wei­li­ge Wahr­schein­lich­keit, eine be­stimm­te Zahl zu er­rei­chen?
    Schrei­be die Wahr­schein­lich­kei­ten auf.
Bereitgestellt von: MNWeG Stand: 27.10.2023 Lizenzhinweise: https://editor.mnweg.org/mnw/dokument/zufallsexperimente-6
Seite: 3/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/mnw/dokument/zufallsexperimente-6

Zufallsexperimente

von MNWeG
Mathematik
Wahrscheinlichkeit
M (Mindeststandard)
9
Einzelarbeit
Arbeitsblatt
27.10.2023
Mehr entdecken:

Lizenzhinweis

Alle Bestandteile dieses Materials sind frei oder unlizenziert. Klicken Sie auf einen Baustein, um die Lizenz zu sehen.
x