Ist ja klar!
Die Spielkarte ist achsensymmetrisch, man kann sie einfach in der Mitte knicken und dann liegen gleiche Bilder aufeinander!
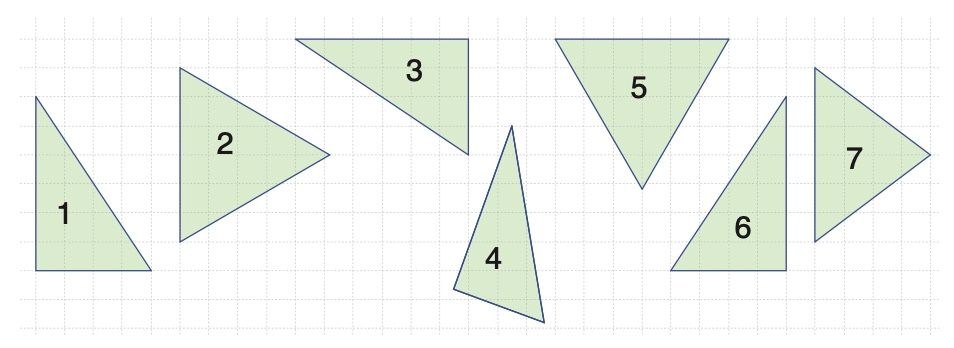
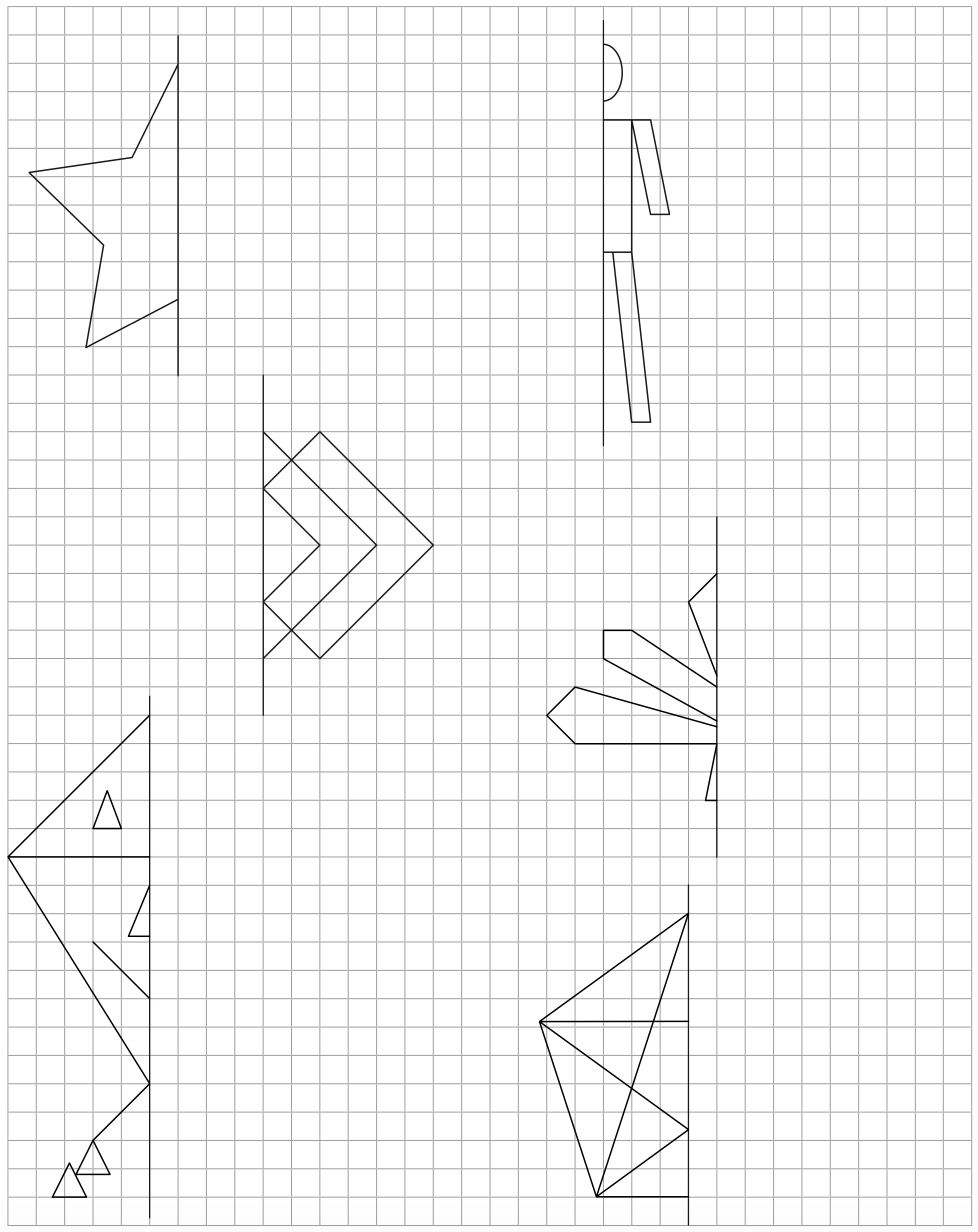
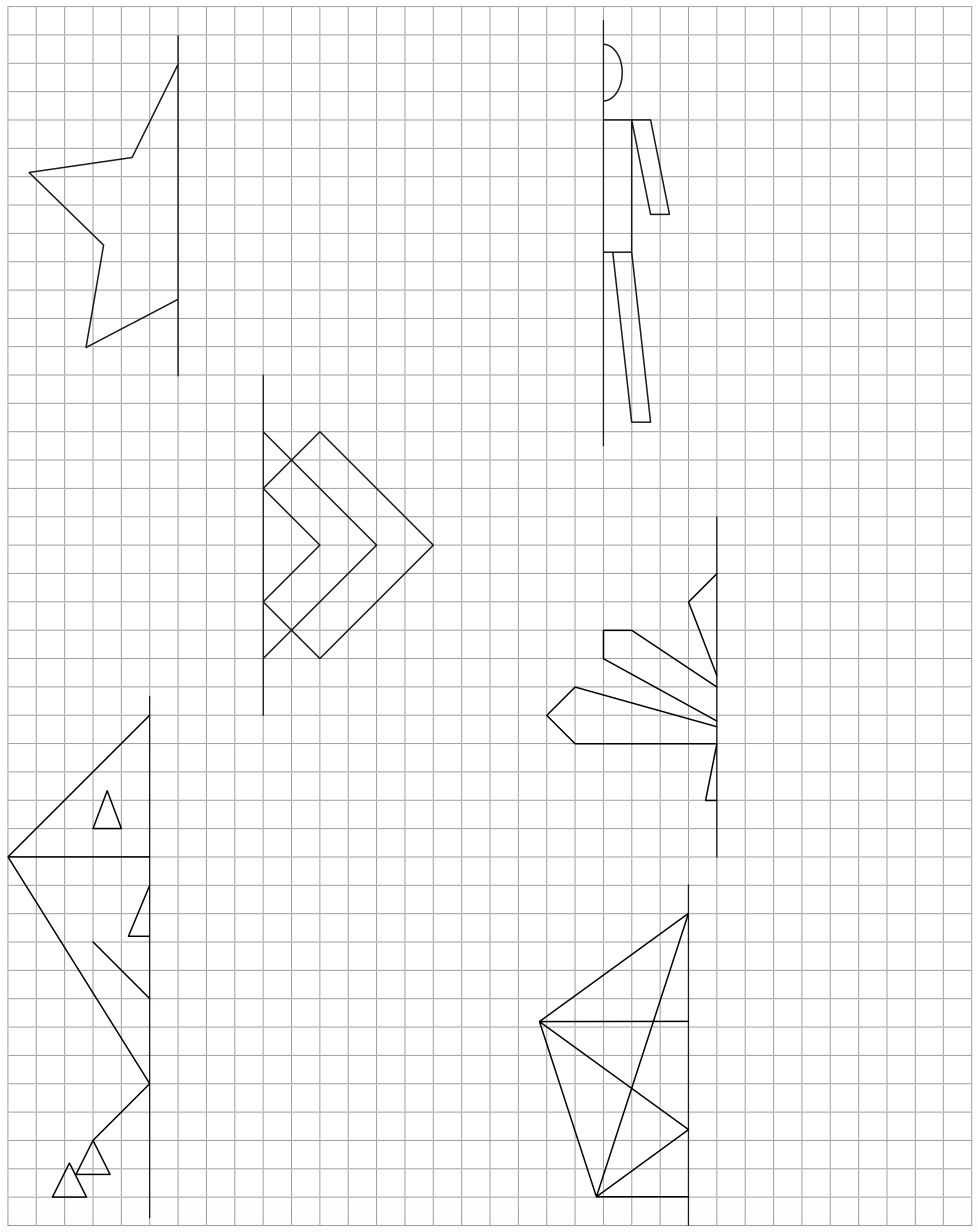
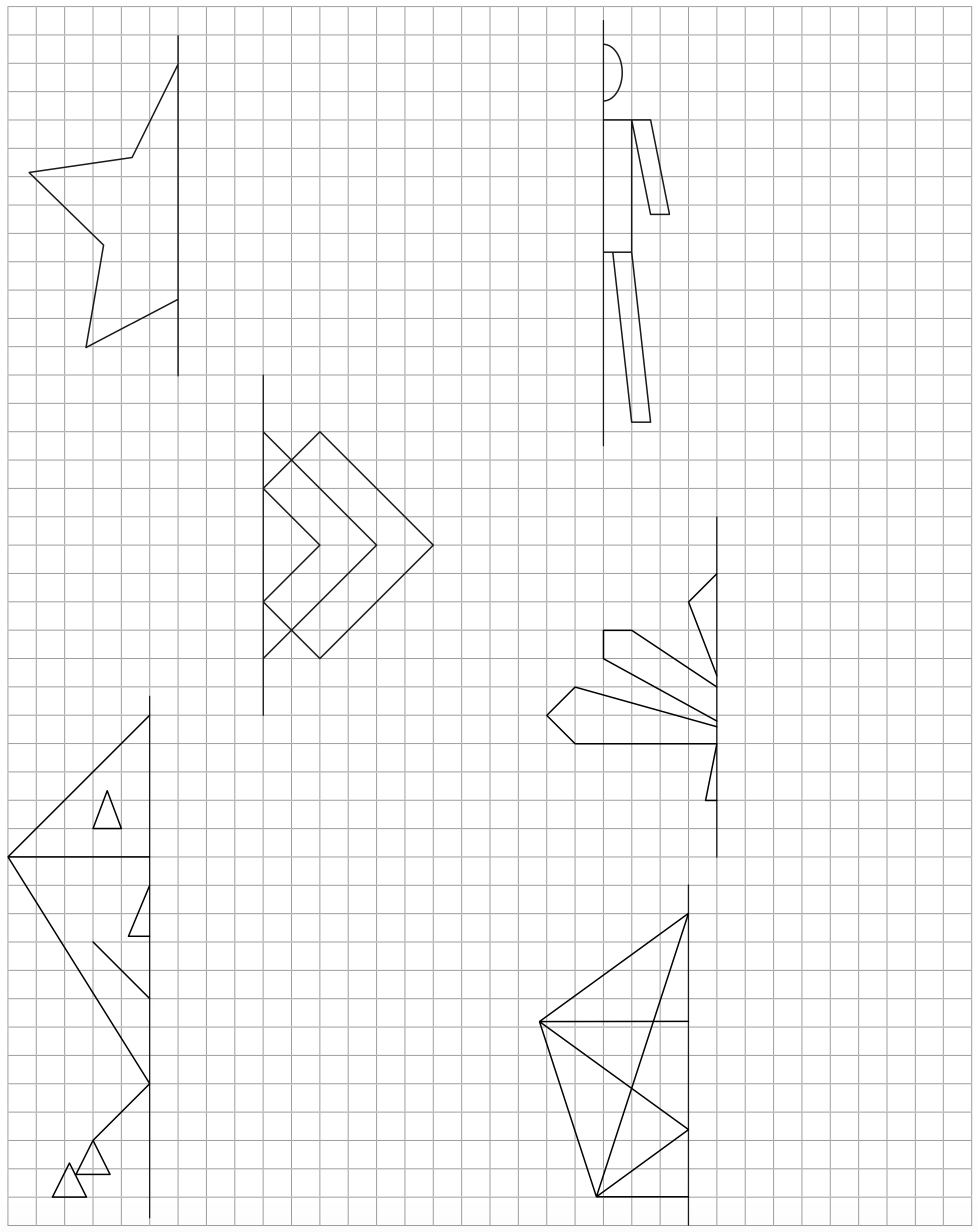


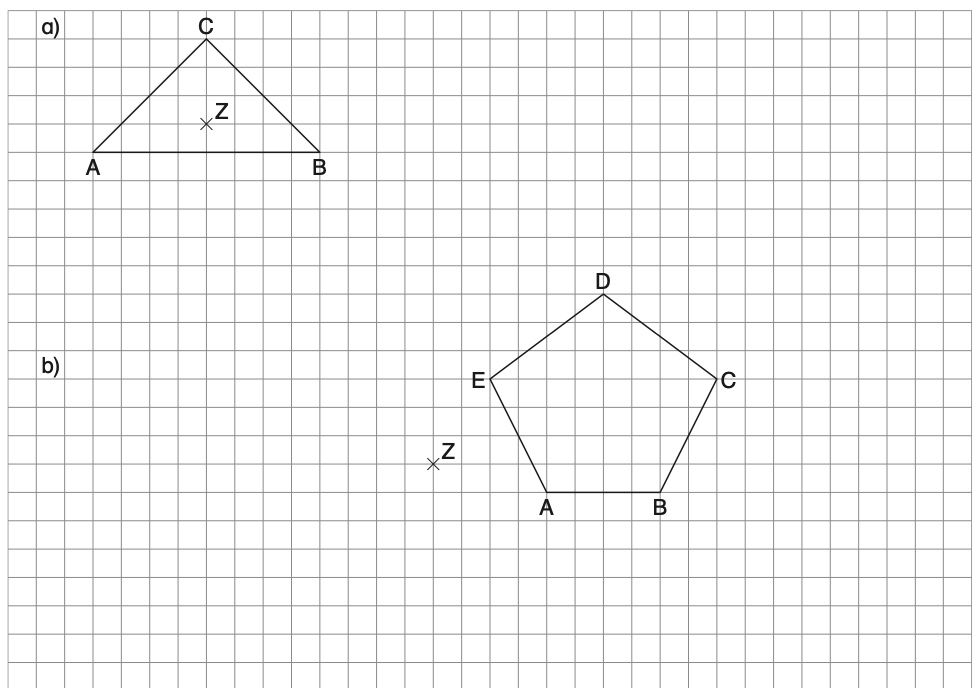


Ist ja klar!
Die Spielkarte ist achsensymmetrisch, man kann sie einfach in der Mitte knicken und dann liegen gleiche Bilder aufeinander!
Sie nutzen einen Browser mit dem mnweg.org nicht einwandfrei funktioniert. Bitte aktualisieren Sie Ihren Browser.
Sie verwenden eine ältere Version Ihres Browsers. Es ist möglich, dass mnweg.org mit dieser Version nicht einwandfrei funktioniert. Um mnweg.org optimal nutzen zu können, aktualisieren Sie bitte Ihren Browser oder installieren Sie einen dieser kostenlosen Browser: