Wiederholung: Umgekehrt proportionale Zuordnungen
Ein Handwerker braucht natürlich länger. Klar - oder? Und zwar in diesem Fall dreimal so lang, also 2 Tage mal 3 = 6 Tage.
Das nannten wie umgekehrt proportionale Zuordnung oder antiproportionale Zuordnung.
Zuordnung:
Anzahl Handwerker benötigte Zeit für eine bestimmte Arbeit in Tage
Übertrage die Tabelle und setze sie für 2 und 4 Handwerker fort.
Anzahl Handwerker
3
1
2
4
5
6
Zeit in Tage
2
6
2
1,5
1,2
1
- Wie verändert sich die Zeit, wenn sich die Zahl der Arbeiter verdoppelt, verdreifacht? die Zeit halbiert, drittelt..sich
- Wie verändert sich die Zeit, wenn sich die Zahl der Arbeiter halbiert, drittelt? die Zeit verdoppelt, verdreifacht.....sich
(Antiproportionale Zuordnung)
Für eine umgekehrt proportionale Zuordnung gilt:
Verdoppelt, verdreifacht sich die erste Größe (Ausgangsgröße), so halbiert, drittelt sich die zweite Größe (zugeordnete Größe) usw..
Halbiert sich die erste Größe, so verdoppelt sich die zweite Größe usw.
Neues entdecken
Notiere deine Beobachtung. Kreuze liegen nicht mehr auf einer Geraden
Ordnen und Informieren
Verbindet man die Kreuze im Koordinatensystem, entsteht eine Kurve, die die Achsen nie berühren wird.
Den Graph bezeichnet man als Hyperbel.
Dann lies im Lehrbuch Schnittpunkt Klasse 7 auf Seite 165 oder schau dir das Erklärvideo an.
Notieren
Schreibe unter der Überschrift 8. Umgekehrt porportionale Zuordnungen darstellen selbständig im Merkteil auf, wie der Graph von umgekehrt proportionalen Zuordnungen aussieht und zeichne eine Hyperbel.
Üben
- Vervollständige die Tabelle.
- Zeichne das Schaubild.
Anzahl der Reihen
2
3
4
5
6
10
12
15
20
30
Anzahl der Karten je Reihe
30
20
15
12
10
6
5
4
3
2
x-Achse: 1 Kästchen für 1 Reihe
y-Achse: 1 Kästchen für 1 Karte
Achtung: Die Punkte werden eigentlich nicht verbunden, da hier nur ganze Zahlen möglich sind.
Anzahl der Pumpen
1
2
3
4
6
Zeit in h
48
24
16
12
8
- Schreibe in einer Tabelle fünf Wertepaare aus der Anzahl der Stücke und der Länge eines Stücks auf.
Beispiel: 24 m : 2 = 12 m; also (2; 12) - Zeichne ein Schaubild.
- Lies in deinem Schaubild ab:
Wie lang ist ein Stück, wenn man das Band in 5; 10 bzw. 16 Stücke teilt.
Anzahl der Stücke
2
3
4
6
12
Länge eines Stücks in m
12
8
6
4
2
Das heißt: Wenn das Band in 5 Stücke geteilt wird, ist ein Stück 4,8m lang; wird das Band in 10 Stücke geteilt, so ist ein Stück 2,4m lang und bei einer Teilung in 16 Stücke ist ein Stück 1,5m lang.
Geschwindigkeit in km/h
10
20
30
60
120
180
Zeit in s
180
90
60
30
15
10
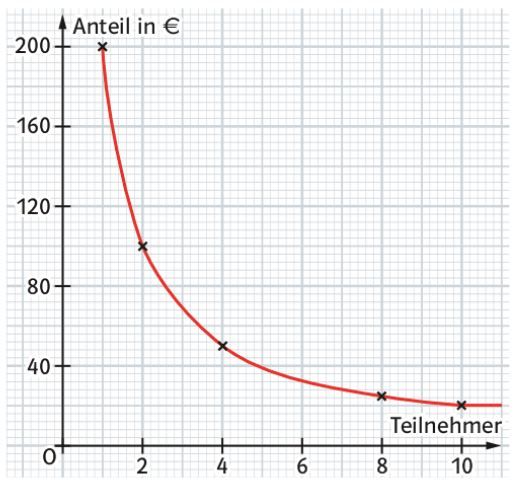
- Trage die Wertepaare in eine Tabelle ein. Nenne einen passenden Sachverhalt.
- Gib den Anteil in € für 6 Teilnehmer an.
Bestimme die Anzahl der Teilnehmer bei einem Anteil von 66,66 €.
Teilnehmer
1
2
4
8
10
Anteil in €
200
100
50
25
20
• Es wird eine Gruppenreise mit einem Kleinbus organisiert. Für den Bus muss eine feste Pauschale von 200 € gezahlt werden. Die Kosten werden auf die Teilnehmer umgelegt.
• Eine Gruppe Personen gewinnt beim Lotto 200 €. Der Lotteriegewinn wird an die Teilnehmer der Gruppe verteilt.
b)
200 € : 6 ≈ 33,33 €
Bei 6 Personen beträgt der Anteil pro Person 33,33 €.
200 € : 66,66 € ≈ 3,0
Bei einem Anteil von 66,66 € sind es 3 Teilnehmer.
Hinweis: Die Ergebnisse können berechnet oder aus dem Schaubild abgelesen werden.
- Vervollständige.
Je mehr Reinigungskräfte in dem Schulgelände arbeiten, weniger Zeit benötigen sie.
Wenn die Reinigung schneller beendet sein soll, dann müssen mehr Personen arbeiten.
Das ist eine umgekehrt proportionale Zuordnung. - Heute sind 9 Reinigungskärfte für ein anderes Projekt eingeteilt.
Gib die Anzahl der Personen an, die die Schule heute putzen. 9 Personen
Bestimme die Zeit, die die verkleinerte Mannschaft benötigt. 8 Stunden
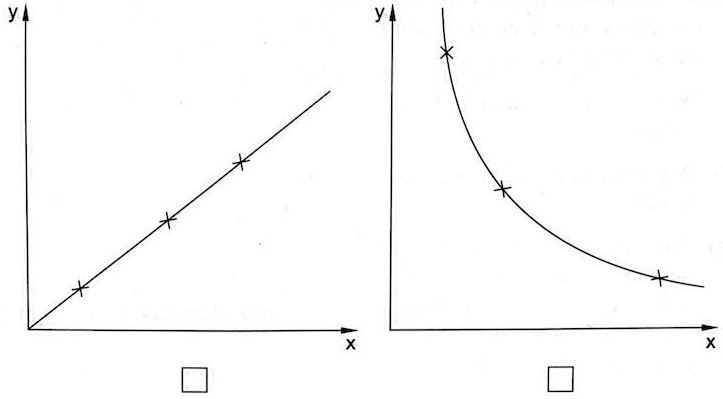
Gib die zeit an,. die eine einzige Reinigungskraft an der Schule putzen würde. 72 Stunden - Ordne die passende Darstellung zur beschriebenen Situation zu.
Überprüfe deinen Lernerfolg
Proportionale oder umgekehrt proportionale Zuordnung.
Zeige deinen Lernerfolg einem Lernbegleiter und lass dir
zum Thema Umgekehrt proportionale ZO darstellen" ein + geben.
