Mit einem Zahlenstrahl oder einer Zahlengeraden lassen sich Zahlen übersichtlich darstellen und leicht vergleichen. Auf dem Zahlenstrahl sind die Zahlen von klein nach groß sortiert. Kleine Zahlen stehen links, große Zahlen stehen rechts. Eine Pfeilspitze am rechten Rand deutet an, dass der Zahlenstrahl beliebig verlängert werden kann.

Gleiche Abstände auf dem Papier bedeuten auch gleiche Abstände zwischen den Zahlen auf dem Zahlenstrahl. Dabei sind jedoch nicht nur Einerschritte erlaubt. Ein Zahlenstrahl kann auch größere Bereiche mit größeren Abständen zwischen den Zahlen darstellen. Dieser Zahlenstrahl hat zum Beispiel Zweierschritte:

Um einen größeren Zahlenbereich darstellen zu können, können auch die Abstände zwischen den Zahlen verringert werden:
Natürlich können auch Fünferschritte oder Zehnerschritte gemacht werden:


Die Zwischenschritte können durch Striche markiert sein, die nicht beschriftet sind:

Im Vergleich zum Zahlenstrahl ist eine Zahlengerade nach links offen. Sie muss nicht bei Null beginnen, sondern kann auch mit einer höheren Zahl anfangen:
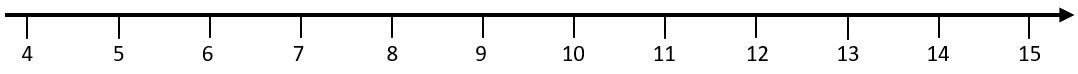
https://editor.mnweg.org/turmbergschule-weingarten-gemeinschaftsschule/dokument/zahlen-ordnen-18
Die Größe von Zahlen vergleichen
Auf dem Zahlenstrahl sind die Zahlen immer der Größe nach sortiert. Ob eine Zahl größer oder kleiner ist, lässt sich mit mathematischen Symbolen beschreiben:
6 > 2 bedeutet: „Die 6 ist größer als die 2.“
3 < 5 bedeutet: „Die 3 ist kleiner als die 5.“
Wenn die Zahlen gleich sind, wird das Gleichheitszeichen (=) verwendet.
> bedeutet „größer als“
< bedeutet „kleiner als“
= bedeutet „gleich“
Vorgänger und Nachfolger
Eine Zahl, die genau um eins größer ist als eine andere Zahl, wird als Nachfolger bezeichnet. So ist der Nachfolger von 3 die 4 und der Nachfolger von 11 ist 12.
Jede natürliche Zahl hat einen Nachfolger, weil es immer möglich ist, plus eins zu rechnen.
Vorgänger sind die Zahlen, die beim Zählen vor einer Zahl kommen. Um den Vorgänger herauszufinden, wird minus eins gerechnet. So ist 5 der Vorgänger von 6 und 9 der Vorgänger von 10.
Außer der Null hat jede natürliche Zahl einen Vorgänger.
4
2
1
3
Die 4 ist der
Nachfolger
der 3.
Die 2 ist der
Vorgänger
der 3.
https://editor.mnweg.org/turmbergschule-weingarten-gemeinschaftsschule/dokument/zahlen-ordnen-18


