Viele zusammengesetzte Körper bestehen aus Quadern und Würfeln. Die Zerlegungslinien sind nicht immer sichtbar.
Das Volumen eines zusammengesetzten Körpers berechnet man, indem man das Volumen der Teilkörper addiert.
Den Oberflächeninhalt eines zusammengesetzten Körper berechnet man, indem man die äußeren Teilflächen addiert.
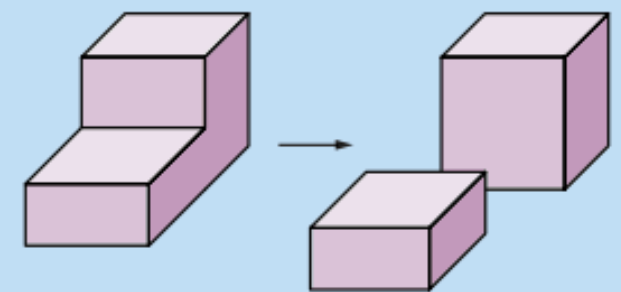
Beispiel 1
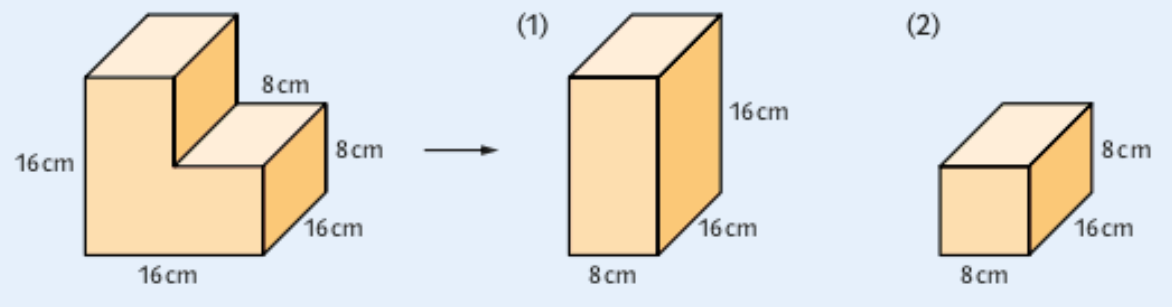
Gesucht ist das Volumen und die Oberfläche des Körpers.
Der Körper kann in zwei Quader zerlegt werden.
Volumen der Teilkörper:
Quader (1)
V=8⋅16⋅16cm3
V=2048cm3
Quader (2)
V=8⋅16⋅8cm3
V=1024cm3
Gesamtvolumen =
Volumen Quader 1 + Volumen Quader 2
V=2048cm3+1024cm3
V=3072cm3
Das Gesamtvolumen des Körpers beträgt 3072 cm³
https://editor.mnweg.org/turmbergschule-weingarten-gemeinschaftsschule/dokument/zusammengesetzte-koerper-1
Die Oberfläche des Körpers besteht aus der Vorder- und Rückfläche, der Fläche links und den Stufenflächen.
Also:
O=A(V+R)+A(l)+4⋅A(Stufe)
Vorder- und Rückfläche:
A(V+R)=16⋅8+8⋅8cm2=192cm2
Fläche links:
A(l)=16⋅16cm2=256cm2
Stufenfläche:
A(S)=16⋅8cm2=128cm2
Oberflächeninhalt
O=192cm2+256cm2+4⋅128cm2
O=960cm2
Der Oberflächeninhalt des zusammengesetzten Körpers beträgt 960 cm²
Beispiel 2
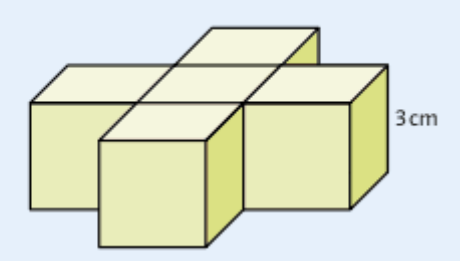
Gesucht ist das Volumen und die Oberfläche des abgebildeten Körpers.
Volumen
Der Körper besteht aus 5 Würfeln mit der Kantenlänge 3 cm.
V=5⋅33cm3
V=5⋅27cm3
V=135cm3
Das Volumen des Körpers beträgt 135 cm³.
Oberfläche
Die Oberfläche des Körpers besteht aus insgesamt 22 Quadraten mit der Seitenlänge 3 cm.
O=22⋅32cm2
O=198cm2
Die Oberfläche des Körpers beträgt 198 cm²
https://editor.mnweg.org/turmbergschule-weingarten-gemeinschaftsschule/dokument/zusammengesetzte-koerper-1


