Der tiefste Punkt der Normalparabel nennt sich Scheitelpunkt.
In diesem Kapitel lernst du ganz unterschiedlich aussehende Parabeln kennen. Du wirst
herausfinden, wie man Parabeln strecken, stauchen und spiegeln kann,
entdecken, welche Parameter es in der Scheitelpunktform quadratischer Funktionen gibt.
Mit diesem Wissen kannst du dann selbst verschiedene Parabeln darstellen und beschreiben.
Quadratische Funktionen verändern
Wenn du dir die Bilder noch einmal anschaust, dann fällt auf, dass die abgebildeten Parabeln anders aussehen als die gerade kennengelernte Normalparabel. In der Natur und in Anwendungen wird der Funktionsterm der Normalparabel (y=x2) variiert und es entstehen die unterschiedlichsten Parabeln.





Eine Anwendung wird dir im folgenden Video gezeigt. Das Deutsche Zentrum für Luft- und Raumfahrt (DLR) führt seit einigen Jahren Parabelflüge durch.
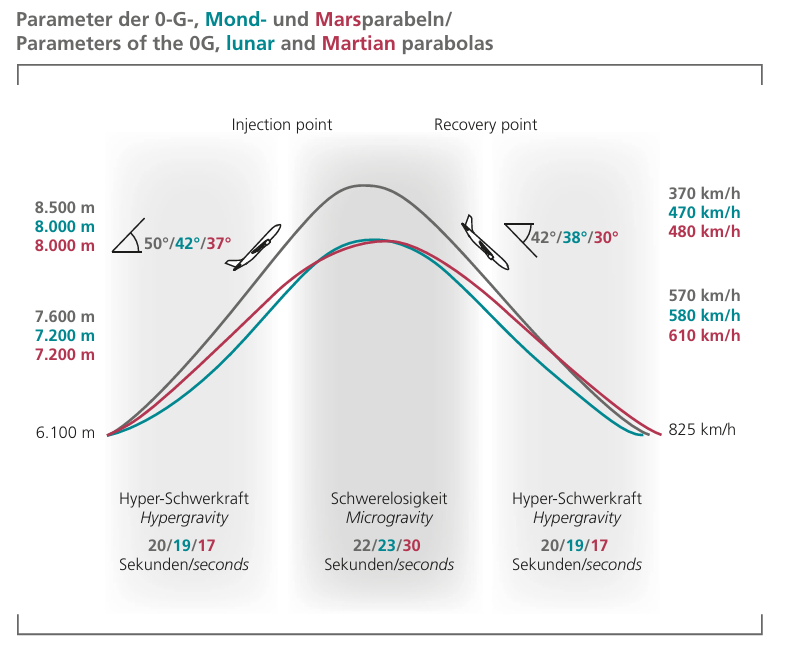
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
Wie sieht der Graph einer Normalparabel aus?
Der Graph einer quadratischen Funktion ist eine Parabel. Der Graph der Funktion f(x)=x2 wird als Normalparabel bezeichnet.
Strecken, Stauchen, Spiegeln: Parameter a
von f(x)=a⋅x2
a von f(x)=a⋅x2
Was passiert, wenn man statt der Funktion y=x2 folgende Funktionen gegeben hat:
y=2x2
y=21x2
y=−x2
Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die drei Funktionen aufstellen und die Funktionswerte mit den Werten von y=x2 vergleichen.
Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen, ohne diese zu zeichnen.
Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen, ohne diese zu zeichnen.
Öffne anschließend das GeoGebra Applet und versuche, deine Vermutungen zu überprüfen.
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
In dem folgenden Lückentext werden die Erkenntnisse, die du aus der Aufgabe mitnehmen konntest, noch einmal ausformuliert. Füge die fehlenden Begriffe und Zahlen in die Lücken.
Wenn a kleiner Null ist (a<0), dann ist die Parabel nach geöffnet.
Wenn a größer Null ist (a>0), dann ist die Parabel nach geöffnet.
Wenn a zwischen minus Eins und Eins liegt (−1<a<1), dann wird der Graph der Funktion . Man nennt das auch eine gestauchte Parabel.
Wenn a kleiner als (a< ) oder größer als ist (a> ), dann wird der Graph der Funktion gestreckt. Er ist somit als die Normalparabel.
Mit dieser APP kannst du mit dem Streckungsfaktor nochmals üben.
Multipliziert man y=x2 mit einem Faktor a, wird die Parabel gestreckt, gestaucht und/oder gespiegelt. y=ax2 (mit a≠0) ergibt demnach für:
a > 0: Die Parabel ist nach oben geöffnet.
a < 0: Die Parabel ist nach unten geöffnet.
|a| > 1: Die Parabel ist gestreckt
|a| < 1: Die Parabel ist gestaucht
Der Parameter a wird auch Streckungsfaktor genannt.
Beispiele:
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
Seitliche Verschiebung der Parabel (Verschiebung in x-Richtung)
Was passiert, wenn man statt der Funktion y=x2 folgende Funktionen gegeben hat:
y=(x−2)2
y=(x+2)2
Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die zwei Funktionen aufstellen und die Funktionswerte mit den Werten von y=x2 vergleichen.
Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen, ohne diese zu zeichnen.
Öffne anschließend das GeoGebra Applet und versuche, deine Vermutungen zu überprüfen.
Addiert oder subtrahiert man eine Zahl d von x vor dem Quadrieren, so wird die Parabel entlang der x-Achse verschoben. Für y=(x−d)2 gilt:
d > 0: Die Parabel wird entlang der x-Achse in positive Richtung verschoben.
d < 0: Die Parabel wird entlang der x-Achse in negative Richtung verschoben.
Um besser zu erkennen, wie sich eine seitliche Verschiebung auswirkt, wird für die Graphen in der folgenden Abbildung die Form f(x)=(x−d)2 gewählt.
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
Lies dir die Unterhaltung von Fabian und Merle durch und versuche, die Begründung nachzuvollziehen.
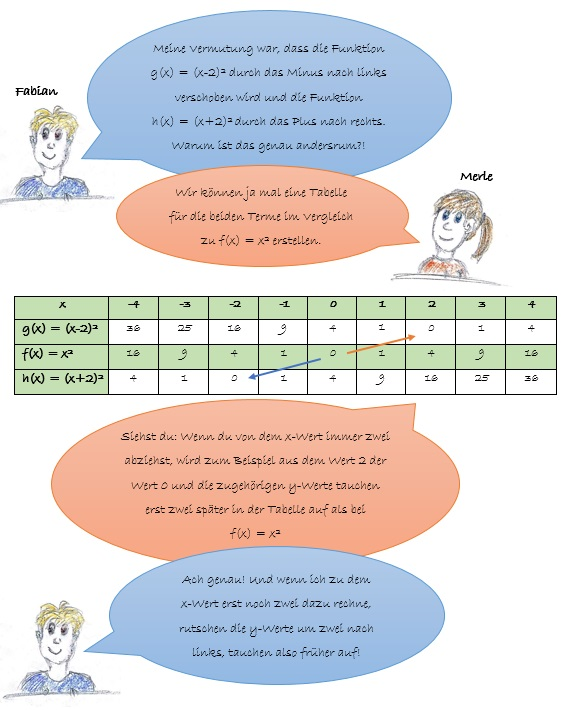
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
Verschiebung nach oben und unten (in y-Richtung)
Was passiert, wenn man statt der Funktion y=x2 folgende Funktionen gegeben hat:
y=x2+3
y=x2−3
Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die zwei Funktionen aufstellen und die Funktionswerte mit den Werten von y=x2 vergleichen.
Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen, ohne diese zu zeichnen.
Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen, ohne diese zu zeichnen.
Öffne anschließend das GeoGebra Applet und versuche, deine Vermutungen zu überprüfen.
Addiert oder subtrahiert man eine Zahl e von y=x2, wird die Parabel entlang der y-Achse verschoben. Für y=x2+e gilt:
e > 0: Die Parabel wird entlang der y-Achse in positive Richtung (nach oben) verschoben.
e < 0: Die Parabel wird entlang der y-Achse in negative Richtung (nach unten) verschoben.
Beispiele:
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
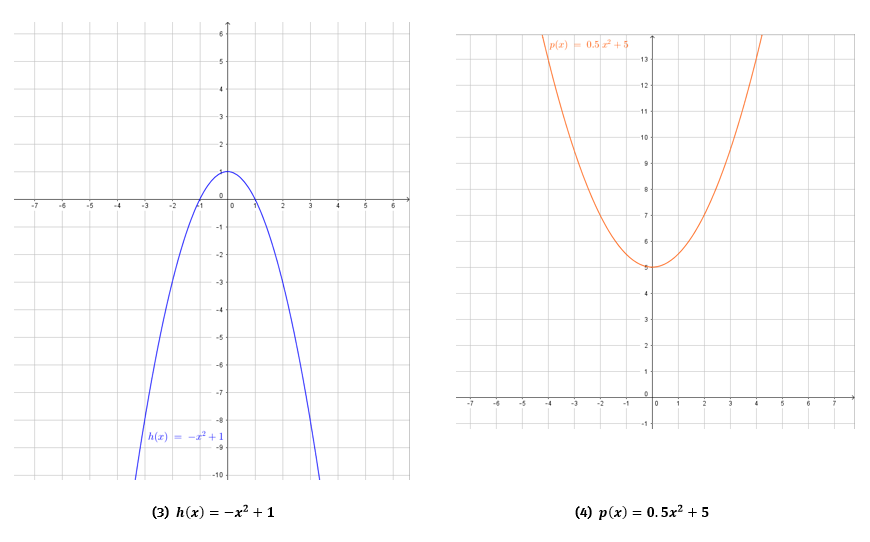
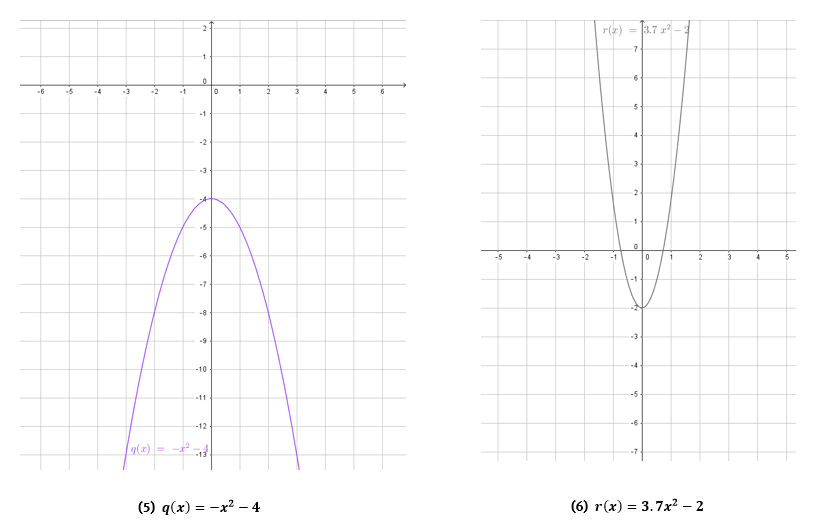
- Zeichne die passenden Koordinatensysteme für drei der quadratischen Funktionen:
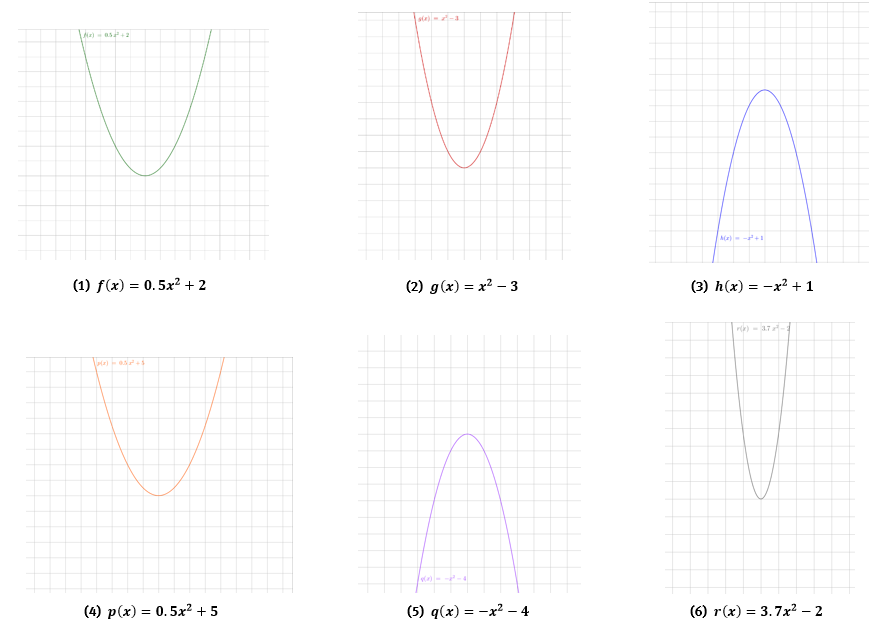
Der Parameter d kommt bei keiner der Parabeln vor, das heißt der Graph ist weder nach rechts noch nach links verschoben.
Der Parameter a sorgt für eine Stauchung oder Streckung der Parabel. Der Parameter e verschiebt die Parabel in y-Richtung, also entlang der y-Achse nach oben oder unten.
Nutze für die Abstände auf der x- und y-Achse jeweils 1 Kästchen und gehe in Einserschritten voran.
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
Lösungen
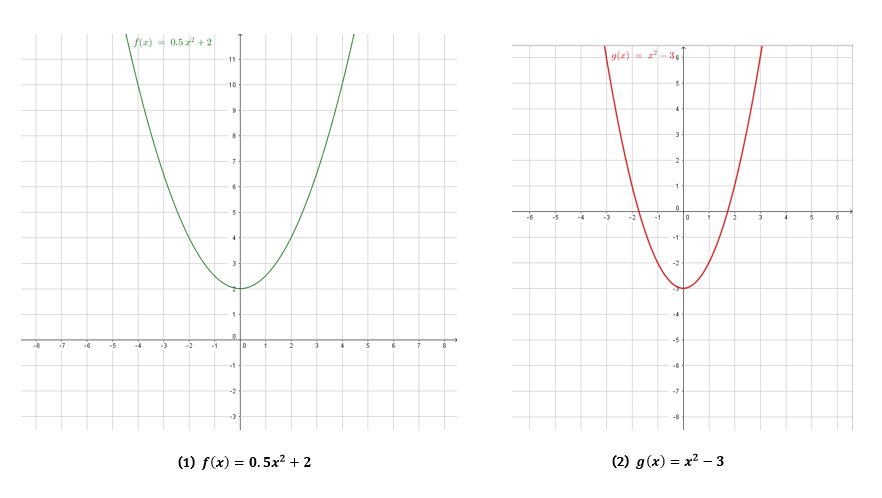
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen
https://editor.mnweg.org/entdecken/dokument/parameter-quadratischer-funktionen


